题目内容
10. 如图,已知△ABC的周长为24,OB,OC分别平分∠ABC,∠ACB,OD⊥BC于点D,且OD=2,求△ABC的面积.
如图,已知△ABC的周长为24,OB,OC分别平分∠ABC,∠ACB,OD⊥BC于点D,且OD=2,求△ABC的面积.
分析 连接OA,作OE⊥AB于E,OF⊥AC与F,根据角平分线的性质求出OE、OF的长,根据△ABC的面积=△A0B的面积+△BOC的面积+△AOC的面积计算即可.
解答  解:连接OA,作OE⊥AB于E,OF⊥AC与F,
解:连接OA,作OE⊥AB于E,OF⊥AC与F,
∵OB,OC分别平分∠ABC,∠ACB,OD⊥BC,OE⊥AB,OF⊥AC,
∴OE=OE=OD=2,
△ABC的面积=△A0B的面积+△BOC的面积+△AOC的面积
=$\frac{1}{2}$AB•OE+$\frac{1}{2}$AC•OF+$\frac{1}{2}$CB•OD
=$\frac{1}{2}$×(AB+AC+BC)×2
=24.
答:△ABC的面积是24.
点评 本题主要考查平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键,注意辅助线的作法要正确.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
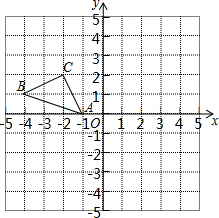 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
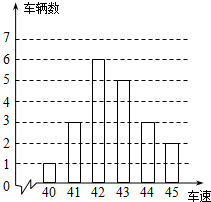 已知:如图,是交警在某个路口统计的某时段来往车辆的车速(单位:千米/时)情况.
已知:如图,是交警在某个路口统计的某时段来往车辆的车速(单位:千米/时)情况. 如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=BC=8cm,BD=5cm,则点D到AB的距离是3cm.
如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=BC=8cm,BD=5cm,则点D到AB的距离是3cm.