题目内容
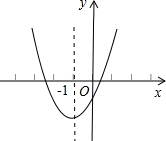 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为x=-1,给出下列结论:①abc>0;②2a+b=0;③a+b+c>0;④a-b+c<0,其中正确的结论是( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为x=-1,给出下列结论:①abc>0;②2a+b=0;③a+b+c>0;④a-b+c<0,其中正确的结论是( )| A、①② | B、①④ | C、②③ | D、③④ |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线开口方向得到a>0,由抛物线的对称轴为直线x=-
=1得到b=2a>0,由抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;由x=1时,函数值为正数得到a+b+c>0;由x=-1时,函数值为负数得到a-b+c<0.
| b |
| 2a |
解答:解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵b=2a,
∴2a-b=0,所以②错误;
∵x=1时,y>0,
∴a+b+c>0,所以③正确;
∵x=-1时,y<0,
∴a-b+c<0,所以④正确.
故答案为:③④.

∴a>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵b=2a,
∴2a-b=0,所以②错误;
∵x=1时,y>0,
∴a+b+c>0,所以③正确;
∵x=-1时,y<0,
∴a-b+c<0,所以④正确.
故答案为:③④.
点评:本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
一个三角形任意一边上的高都是这边上的中线,则对这个三角形最准确的判断是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )
如图,把一张长方形纸沿对角线AC折叠后,顶点B落在B′处,已知∠ACB′=28°,那么,∠DCB′=( )| A、28° | B、31° |
| C、32° | D、34° |
 如图所示,已知AB∥CD,∠1=∠2,试说明∠E=∠F,写出你的推理过程.
如图所示,已知AB∥CD,∠1=∠2,试说明∠E=∠F,写出你的推理过程.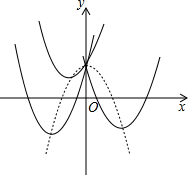 已知二次函数y=2x2+bc+1(b为常数),当b取不同的值时,其图象构成一个“抛物线系”,图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),这条抛物线的解析式是
已知二次函数y=2x2+bc+1(b为常数),当b取不同的值时,其图象构成一个“抛物线系”,图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),这条抛物线的解析式是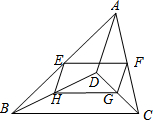 如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
如图,D是△ABC内一点,BD⊥CD,AD=12,BD=8,CD=6,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )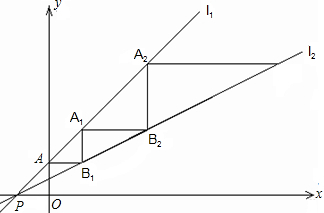 如图,直线l1:y=x+1与直线l2:y=
如图,直线l1:y=x+1与直线l2:y=