题目内容
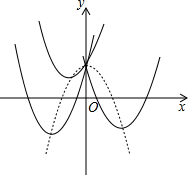已知二次函数y=2x2+bc+1（b为常数），当b取不同的值时，其图象构成一个“抛物线系”，图中的实线型抛物线分别是b取三个不同的值时二次函数的图象，它们的顶点在一条抛物线上（图中虚线型抛物线），这条抛物线的解析式是考点：二次函数的性质
专题：
分析：首先利用b抛物线的顶点坐标，然后变形即可得到所求抛物线的解析式．
解答：解：∵y=2x2+bx+1的顶点坐标是（-
，
），
设x=-
，y=
，
∴b=-4x，
∴y=
=
=1-2x2．
所求解析式为：y=1-2x2，即y=-2x2+1．
故答案为：y=-2x2+1．
| b |
| 4 |
| 8-b2 |
| 8 |
设x=-
| b |
| 4 |
| 8-b2 |
| 8 |
∴b=-4x，
∴y=
| 8-b2 |
| 8 |
| 8-(-4x)2 |
| 8 |
所求解析式为：y=1-2x2，即y=-2x2+1．
故答案为：y=-2x2+1．
点评：此题主要考查了二次函数的性质，首先利用抛物线的顶点坐标公式，然后进行代数变形即可求解．
练习册系列答案
相关题目
如图，点C在线段AB上，线段AC=4cm，BC=6cm．已知a＜0，b＞0，在a+b，a-b，-a+b，-a-b中最大的是（ ）
| A、a+b | B、a-b |
| C、-a+b | D、-a-b |
二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：某班30名学生身高检测结果如下表（单位：米），则该班学生身高的众数是（ ）
| 身高 | 1.57 | 1.58 | 1.59 | 1.60 | 1.61 | 1.62 | 1.63 | 1.64 |
| 人数 | 2 | 2 | 3 | 3 | 8 | 7 | 3 | 2 |
| A、1.59 | B、1.60 |
| C、1.61 | D、1.62 |
如图，抛物线y=mx2-2mx-3m（m＞0）与x轴交于A、B两点，与y轴交于C点．
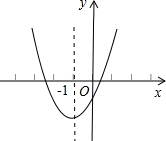已知二次函数y=ax2+bx+c的图象如图所示，其对称轴为x=-1，给出下列结论：①abc＞0；②2a+b=0；③a+b+c＞0；④a-b+c＜0，其中正确的结论是（ ）| A、①② | B、①④ | C、②③ | D、③④ |
