题目内容
一个三角形任意一边上的高都是这边上的中线，则对这个三角形最准确的判断是（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
考点：等边三角形的判定
专题：
分析：根据等腰三角形的性质易得这个三角形的三边都相等，然后根据等边三角形的判定方法可得这个三角形必为等边三角形．
解答：解：∵一个三角形任意一边上的高都是这边上的中线，
即三角形任意一边上的高与中线重合，
∴这个三角形的三边都相等，
∴这个三角形必为等边三角形．
故选D．
即三角形任意一边上的高与中线重合，
∴这个三角形的三边都相等，
∴这个三角形必为等边三角形．
故选D．
点评：本题考查了等边三角形的判定：三条边都相等的三角形是等边三角形；三个角都相等的三角形是等边三角形；有一个角是60°的等腰三角形是等边三角形．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
（-7）2的算术平方根是（ ）
| A、+7 | ||
| B、±7 | ||
C、
| ||
D、±
|
△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于点D，若BC=a，则AD等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，点C在线段AB上，线段AC=4cm，BC=6cm．
如图，∠1=30°，∠2=70°，则∠3=
如图，是两块边长分别为a、b的黑色正方形瓷砖和两块白色的长方形瓷砖拼成的无缝图案．若频率为0.2，总数为100，则频数为（ ）
| A、0.2 | B、200 |
| C、100 | D、20 |
已知a＜0，b＞0，在a+b，a-b，-a+b，-a-b中最大的是（ ）
| A、a+b | B、a-b |
| C、-a+b | D、-a-b |
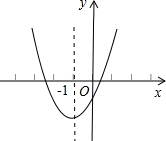已知二次函数y=ax2+bx+c的图象如图所示，其对称轴为x=-1，给出下列结论：①abc＞0；②2a+b=0；③a+b+c＞0；④a-b+c＜0，其中正确的结论是（ ）