题目内容
2.若分式$\frac{1}{x-5}$有意义,则x的取值范围是x≠5;当x=1时,分式$\frac{{{x^2}-1}}{x+1}$的值为0.分析 分式有意义的条件是分母不等于零;分式值为零的条件是分子等于零且分母不等于零.
解答 解:∵分式$\frac{1}{x-5}$有意义,
∴x-5≠0.
解得:x≠5.
$\frac{{{x^2}-1}}{x+1}$=$\frac{(x+1)(x-1)}{x+1}$=x-1.
∵分式$\frac{{{x^2}-1}}{x+1}$的值为0,
∴x-1=0.
解得:x=1.
故答案为:x≠5;1.
点评 本题主要考查的是分式值为零和分式有意义的条件,掌握分式值为零和分式有意义的条件是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.两种移动电话计费方式表如下:
(1)一个月内某用户在本地通话时间为x分钟,请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用.
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
| 全球通 | 神州行 | |
| 月租费 | 15元/月 | 0 |
| 本地通话费 | 0.10元/分 | 0.20元/分 |
(2)若某用户一个月内本地通话时间为5个小时,你认为采用哪种方式较为合算?
 如图,经过平移,将的顶点A移到了点D,请作出平移后图形.
如图,经过平移,将的顶点A移到了点D,请作出平移后图形.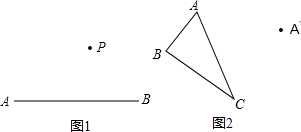
 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2016个等腰直角三角形的斜边长是21008.
如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2016个等腰直角三角形的斜边长是21008.