题目内容
(1)解不等式组
(2)化简(1+
)÷
,并从x=1,2,-5,-2中任选一个你喜欢的数x代入求值.
|
(2)化简(1+
| 1 |
| x-2 |
| x2-2x+1 |
| x2-4 |
考点:解一元一次不等式组,分式的化简求值
专题:
分析:(1)先求出每个不等式的解集,再找出不等式组的解集即可;
(2)先算加法,把除法变成乘法,进行计算,最后选取适当的数代入即可.
(2)先算加法,把除法变成乘法,进行计算,最后选取适当的数代入即可.
解答:解:(1)
由①得:x-3x+6≤4,
-2x≤-2,
x≥1,
由②得:1+2x>3x-3,
-x>-4,
x<4,
所以,原不等式组的解集为1≤x<4;
(2)(1+
)÷
=
÷
=
•
=
,
∵x-2≠0且x-1≠0且x+2≠0,
∴x≠2,x≠1,x≠-2,
∴取x=-5,
当x=-5时,原式=
=
.
|
由①得:x-3x+6≤4,
-2x≤-2,
x≥1,
由②得:1+2x>3x-3,
-x>-4,
x<4,
所以,原不等式组的解集为1≤x<4;
(2)(1+
| 1 |
| x-2 |
| x2-2x+1 |
| x2-4 |
=
| x-2+1 |
| x-2 |
| (x-1)2 |
| (x+2)(x-2) |
=
| x-1 |
| x-2 |
| (x+2)(x-2) |
| (x-1)2 |
=
| x+2 |
| x-1 |
∵x-2≠0且x-1≠0且x+2≠0,
∴x≠2,x≠1,x≠-2,
∴取x=-5,
当x=-5时,原式=
| -5+2 |
| -5-1 |
| 1 |
| 2 |
点评:本题考查了解一元一次不等式组,分式的混合运算和求值,分式有意义的条件的应用,(1)小题的关键是能关键不等式的解集找出不等式组的解集,(2)小题的关键是能正确的进行化简,难度适中.

练习册系列答案
相关题目
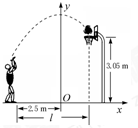 小敏在某次投篮中,球的运动线路是抛物线y=-
小敏在某次投篮中,球的运动线路是抛物线y=-| 1 |
| 5 |
| A、3.5m | B、4m |
| C、4.5m | D、4.6m |
反比例函数y=
,当x<0时,y随x的增大而减小,则k的取值范围为( )
| 2k+4 |
| x |
| A、k>0 | B、k<0 |
| C、k>-2 | D、k<-2 |
如果分式
的值为零,那么x等于( )
| |x|-1 |
| x-1 |
| A、1 | B、-1 | C、0 | D、±1 |