题目内容
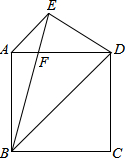 如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.
如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.考点:正方形的性质,等腰三角形的性质,含30度角的直角三角形
专题:证明题
分析:连接AC,交BD于点O,作EG⊥BD于点G,则可知四边形AOGE是矩形,可证得EG=
BD=
BE,所以∠EBD=30°,结合条件可求得∠BED=75°,∠EFD=∠FDB+∠EBD=45+30=75°,故∠DEF=∠DFE,即可得到DF=DE.
| 1 |
| 2 |
| 1 |
| 2 |
解答: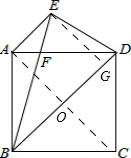 证明:连接AC,交BD于点O,作EG⊥BD于点G.
证明:连接AC,交BD于点O,作EG⊥BD于点G.
∵四边形ABCD是正方形,
∴AC⊥BD,
∵AE∥BD,
∴四边形AOGE是矩形,
∴EG=AO=
AC=
BD=
BE,
∴∠EBD=30°,
∵∠EBD=30°,BE=BD,
∴∠BED=75°,
∵∠EFD=∠FDB+∠EBD=45+30=75°,
∴∠DEF=∠DFE,
∴DF=DE.
 证明:连接AC,交BD于点O,作EG⊥BD于点G.
证明:连接AC,交BD于点O,作EG⊥BD于点G.∵四边形ABCD是正方形,
∴AC⊥BD,
∵AE∥BD,
∴四边形AOGE是矩形,
∴EG=AO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EBD=30°,
∵∠EBD=30°,BE=BD,
∴∠BED=75°,
∵∠EFD=∠FDB+∠EBD=45+30=75°,
∴∠DEF=∠DFE,
∴DF=DE.
点评:本题主要考查正方形的性质及等腰三角形的性质的应用,解题的关键是作出辅助线求得∠EBD=30°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
使式子|2013+m|=|-2013|+|m|成立的m必为( )
| A、正数 | B、负数 |
| C、正数或零 | D、负数或零 |
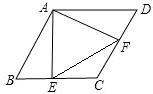 如图,在菱形ABCD中,E、F分别是CB、CD上的点,BE=DF,连接E、F,若E、F分别是CB、CD的中点,△AEF为等边三角形.求证:AE垂直平分BC.
如图,在菱形ABCD中,E、F分别是CB、CD上的点,BE=DF,连接E、F,若E、F分别是CB、CD的中点,△AEF为等边三角形.求证:AE垂直平分BC.