题目内容
已知x2+y2-xy+2x-y+1=0,求x,y的值.
考点:非负数的性质:偶次方
专题:
分析:把x2+y2-xy+2x-y+1=0进行变形,得出(x+1)2=0,(x-2y+1)2=0,再根据非负数的性质即可得出x,y的值.
解答:解:∵x2+y2-xy+2x-y+1=0,
∴
=0,
∴(x+1)2=0,(x-2y+1)2=0,
∴x=-1,y=0.
∴
| [3(x+1)2+(x-2y+1)2] |
| 4 |
∴(x+1)2=0,(x-2y+1)2=0,
∴x=-1,y=0.
点评:此题考查了非负数的性质,关键是把给出的式子进行变形,求出x,y的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
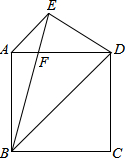 如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.
如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF. 如图,在梯形ABCD中,AB∥CD∥MN,求证:OM=ON.
如图,在梯形ABCD中,AB∥CD∥MN,求证:OM=ON.