Question

6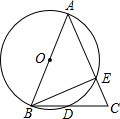．已知；如图，AB是⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，给出以下五个结论：①∠EBC=22.5°；②BD=DC；③$\widehat{BD}$=$\widehat{DE}$；④AE=BC；其中正确结论的序号是①②③．

Answer 1

分析 根据圆周角定理，等边对等角，等腰三角形的性质，直径对的圆周角是直角等知识，得出①②③正确，④错误即可．

解答 解：连接AD，AB是直径，
则AD⊥BC，
又∵△ABC是等腰三角形，
故点D是BC的中点，即BD=CD，故②正确；
∵AD是∠BAC的平分线，
∴∠BAD=∠CAD，∴$\widehat{BD}$=$\widehat{DE}$，③正确；
由圆周角定理知，∠EBC=∠DAC=$\frac{1}{2}$∠BAC=22.5°，故①正确；
∵∠ABE=90°-∠EBC-∠BAD=45°=2∠CAD，故④正确；
∵AE=BE，BE是直角边，BC是斜边，肯定不等，故④错误．
综上所述，正确的结论是：①②③．
故答案为：①②③．

点评 本题考查了圆周角定理，圆心角、弧、弦的关系、等腰三角形的判定与性质以及弧长关系等．熟练掌握等腰三角形的性质和有关定理是解决问题的关键．