题目内容
11.抛物线y=(a+1)x2+2(a+1)x+a2-1只经过三个象限,则a的取值范围是a<-1或a>1.分析 因其对称轴为x=-1,当开口向上时抛物线与y轴的交点在x轴上方,当开口向下时抛物线与y轴的交点在x轴下方时满足条件,分别可求得a的范围.
解答 解:
∵y=(a+1)x2+2(a+1)x+a2-1,
∴抛物线对称轴为x=-1,
当a+1>0即a>-1时,抛物线开口向上,
要使其图象只经过三个象限,则有a2-1>0即可,
即a-1>0,解得a>1,
当a+1<0即a<-1时,抛物线开口向下,
要使其图象只经过三个象限,则有a2-1<0即可,
即a-1<0,解得a<1,
此时a<-1,
综上可知a的取值范围为a<-1或a>1,
故答案为:a<-1或a>1.
点评 本题主要考查二次函数的图象,由二次函数图象经过三个象限得出关于a的不等式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下表为100粒种子的发芽情况:
用统计图说明该种子的发芽率,可选择扇形统计图,说明种子发芽数量,可选择条形统计图;反映种子的发芽规律,可选择折线统计图.
| 天数 | 1 | 2 | 3 | 4 | 5 |
| 发芽数 | 10 | 65 | 15 | 5 | 5 |

 如图,在平行四边形ABCD中,AB=8,AD=4,E是AD的中点,在AB上取一点F,使AF=7.求证:△CBF∽△CDE.
如图,在平行四边形ABCD中,AB=8,AD=4,E是AD的中点,在AB上取一点F,使AF=7.求证:△CBF∽△CDE.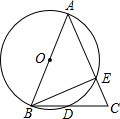 已知;如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③$\widehat{BD}$=$\widehat{DE}$;④AE=BC;其中正确结论的序号是①②③.
已知;如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③$\widehat{BD}$=$\widehat{DE}$;④AE=BC;其中正确结论的序号是①②③.