题目内容
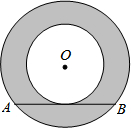 如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2m,则图中阴影部分的面积是( )
如图,两圆圆心相同,大圆的弦AB与小圆相切,AB=2m,则图中阴影部分的面积是( )| A、m2π |
| B、2m2π |
| C、4m2π |
| D、8m2π |
考点:切线的性质,勾股定理,垂径定理
专题:计算题
分析:作OC⊥AB于C,如图,根据垂径定理得AC=BC=
AB=m,在Rt△AOC中利用勾股定理得OA2-OC2=AC2=m2,再根据切线的性质得OC为小圆的半径,所以阴影部分的面积=S大圆-S小圆=π(OA2-OC2)=πm2.
| 1 |
| 2 |
解答:解:作OC⊥AB于C,如图,则AC=BC=
AB=m,
在Rt△AOC中,OA2-OC2=AC2=m2,
,∵大圆的弦AB与小圆相切,
∴OC为小圆的半径,
∴阴影部分的面积=S大圆-S小圆=π•OA2-πOC2=π•(OA2-OC2)=πm2.
故选A.
| 1 |
| 2 |
在Rt△AOC中,OA2-OC2=AC2=m2,
,∵大圆的弦AB与小圆相切,
∴OC为小圆的半径,
∴阴影部分的面积=S大圆-S小圆=π•OA2-πOC2=π•(OA2-OC2)=πm2.
故选A.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常过圆心作切线的垂线段得到圆的半径,利用垂直构造直角三角形解决有关问题.也考查了勾股定理和垂径定理.

练习册系列答案
相关题目
下列各组整式中不是同类项的是( )
| A、3m2n和2m2n | ||
B、2xy2与
| ||
| C、-5ab与-6ab | ||
| D、a与3a |
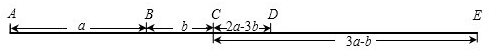
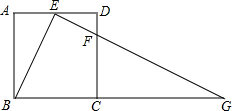 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=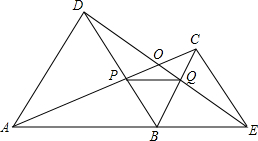 已知△ABD和△BCE均为等边三角形,连接AC,DE交DB于点P,交DE于点O,你能得到哪些结论,并给予证明.
已知△ABD和△BCE均为等边三角形,连接AC,DE交DB于点P,交DE于点O,你能得到哪些结论,并给予证明.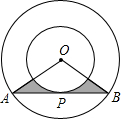 如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是
如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是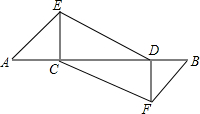 已知AE∥BF,AE=BF,AC=BD.求证:ED=FC.
已知AE∥BF,AE=BF,AC=BD.求证:ED=FC. 如图,点O在直线BC上,∠1与∠2互余,OE平分∠AOC,∠1=27°20′.求∠2,∠3的度数.
如图,点O在直线BC上,∠1与∠2互余,OE平分∠AOC,∠1=27°20′.求∠2,∠3的度数.