题目内容
证明：猜想∠A与∠C关系为：∠A+∠C=180°．
连结AC，
∵∠ABC=90°，
∴在Rt△ABC中，由勾股定理得：
AC=
=25cm，
∵AD2+DC2=625=252=AC2，
∴△ADC是直角三角形，且∠D=90°，
∵∠DAB+∠B+∠BCD+∠D=180°，
∴∠DAB+∠BCD=180°，
即∠A+∠C=180°．
如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：
（1）在图中画一条线段MN，使MN=
；
（2）在图‚中画一个三边长均为无理数，且各边都不相等的直角△DEF．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
B2.,….Bn﹣1为CB的n等分点，连结A1B1，A2B2，…An﹣1Bn﹣1，分别交曲线
（x＞0）于点C1，C2，…，Cn﹣1．若C15B15=16C15A15，则n的值为 ．（n为正整数）
=13，
）求证：AE=BF；
，G为CB中点，连接CF，直接写出四边形CDEF的面积为3．
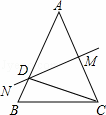
A、B两窗口前面排队的人一样多（设为a人，a＞8），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人．
_____