Question

如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，BF∥DE且交AG于点F．

（1）求证：AE=BF；

（2）如图1，连接DF、CE，探究线段DF与CE的关系并证明；

（3）如图2，若AB=，G为CB中点，连接CF，直接写出四边形CDEF的面积为3．

Answer 1

       （1）证明：∵DE⊥AG于点E，BF∥DE且交AG于点F，

∴BF⊥AG于点F，

∴∠AED=∠BFA=90°，

∵四边形ABCD是正方形，

∴AB=AD且∠BAD=∠ADC=90°，

∴∠BAF+∠EAD=90°，

∵∠EAD+∠ADE=90°，

∴∠BAF=∠ADE，

在△AFB和△DEA中，

，

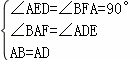∴△AFB≌△DEA（AAS），

∴BF=AE；

（2）DF=CE且DF⊥CE．

理由如下：∵∠FAD+∠ADE=90°，∠EDC+∠ADE=∠ADC=90°，

∴∠FAD=∠EDC，

∵△AFB≌△DEA，

∴AF=DE，

又∵四边形ABCD是正方形，

∴AD=CD，

在△FAD和△EDC中，

，

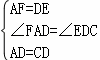∴△FAD≌△EDC（SAS），

∴DF=CE且∠ADF=∠DCE，

∵∠ADF+∠CDF=∠ADC=90°，

∴∠DCF+∠CDF=90°，

∴DF⊥CE；

（3）∵AB=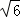，G为CB中点，

∴BG=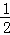BC=，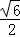

由勾股定理得，AG===，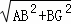

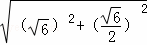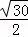∵S_△ABG=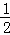AG•BF=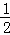AB•BG，

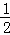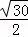∴וBF=××，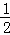

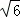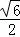解得BF=，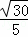

由勾股定理得，AF===，

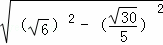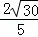∵△AFB≌△DEA，

∴AE=BF=，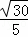

∴AE=EF=，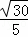

∴DE垂直平分AF，

∴DF=AD=，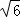

由（2）知，DF=CE且DF⊥CE，

∴四边形CDEF的面积=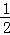DF•CE=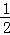××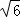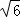=3．