题目内容
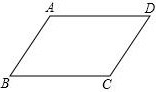已知：如图，在四边形ABCD中，AB∥CD，∠B=∠D．求证：AD∥BC（用两种不同的方法证明）考点：平行线的判定与性质
专题：证明题
分析：方法一：欲证明AD∥BC，只需证得四边形ABCD是平行四边形；方法二：利用平行线的性质“两直线平行，同旁内角互补”和已知条件判定“同旁内角互补”，则两直线平行：AD∥BC．
解答：证明一：如图，∵在四边形ABCD中，AB∥CD，
∴∠B+∠C=180°，∠A+∠D=180°．
又∵∠B=∠D，
∴∠A=∠C，
∴四边形ABCD是平行四边形，
∴AD∥BC；
证明二：如图，∵在四边形ABCD中，AB∥CD，
∴∠A+∠D=180°．
又∠B=∠D，
∴∠A+∠B=180°，
∴AD∥BC．
证明一：如图，∵在四边形ABCD中，AB∥CD，∴∠B+∠C=180°，∠A+∠D=180°．
又∵∠B=∠D，
∴∠A=∠C，
∴四边形ABCD是平行四边形，
∴AD∥BC；
证明二：如图，∵在四边形ABCD中，AB∥CD，
∴∠A+∠D=180°．
又∠B=∠D，
∴∠A+∠B=180°，
∴AD∥BC．
点评：本题考查了平行线的判定与性质．解答此题的关键是注意平行线的性质和判定定理的综合运用．
练习册系列答案
53随堂测系列答案
相关题目
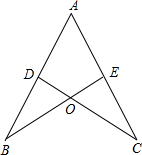如图，AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．
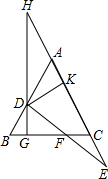已知：如图，在△ABC中，AB=AC，点D，E分别是射线AB，射线AC上一动点，连接DE交BC于点F，且DF=EF，过点D作DG垂直CB于点G，交CA的延长线于点H，当点D在线段AB上，点E在AC的延长线上时，如图所示，先将∠ADH沿直线AD翻折交AC于点K，若∠BAC=60°，CF：CK=3：5，KE=
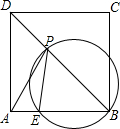如图，正方形ABCD中，AB=4，AE=1，点P是对角线BD上一动点，当△APE的周长最小时，过B，P，E三点的圆的直径为
已知在△ABC中，∠ACB=60°，AC=2，BC=6，将△ABC沿着DE翻折，使点B与点C重合，折痕DE交AB于点D，交BC于点E，那么△ACD的面积为第一小组的同学分铅笔若干支，若每人各取5支，则还剩4支；若有1人只取2支，则其余每人恰好各得6支．若设该小组学生人数为x，铅笔支数为y，则可列方程组（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|