题目内容
因式分解：x3+x2-11x-3．
考点：因式分解
专题：
分析：先拆项，再提取公因式即可．
解答：解：原式=x3-9x+x2-2x-3
=x（x+3）（x-3）+（x+1）（x-3）
=（x-3）[x（x+3）+（x+1）]
=（x-3）（x2+3x+x+1）
=（x-3）（x2+4x+1）．
=x（x+3）（x-3）+（x+1）（x-3）
=（x-3）[x（x+3）+（x+1）]
=（x-3）（x2+3x+x+1）
=（x-3）（x2+4x+1）．
点评：本题考查的是因式分解，在解答此类题目时要注意使用分组分解法．
练习册系列答案
相关题目
方程x（x-5）=0的根是（ ）
| A、x=0 |
| B、x=5 |
| C、x1=0，x2=5 |
| D、x1=0，x2=-5 |
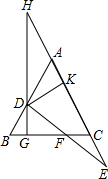已知：如图，在△ABC中，AB=AC，点D，E分别是射线AB，射线AC上一动点，连接DE交BC于点F，且DF=EF，过点D作DG垂直CB于点G，交CA的延长线于点H，当点D在线段AB上，点E在AC的延长线上时，如图所示，先将∠ADH沿直线AD翻折交AC于点K，若∠BAC=60°，CF：CK=3：5，KE=
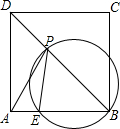如图，正方形ABCD中，AB=4，AE=1，点P是对角线BD上一动点，当△APE的周长最小时，过B，P，E三点的圆的直径为
如图：在△ABC中，AD=AE，BD=EC，∠ADB=∠AEC=105°，∠B=40°，则∠BAC=