题目内容
已知，如图：△ABC中，直线DF分别交BC、AD于D、E，交BA的延长线于点F，且| BD |
| CD |
| BF |
| CE |
考点：相似三角形的判定与性质
专题：证明题
分析：先根据题意得出△BDF∽△CDE，再由相似三角形的对应角相等即可得出结论．
解答：证明：∵
=
，
∴△BDF∽CDE，
∴∠BFD=∠CED．
又∵∠CED=∠AEF，
∴∠BFD=∠AEF，
∴AF=AE．
| BD |
| CD |
| BF |
| CE |
∴△BDF∽CDE，
∴∠BFD=∠CED．
又∵∠CED=∠AEF，
∴∠BFD=∠AEF，
∴AF=AE．
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的对应角相等是解答此题的关键．
练习册系列答案
相关题目
下列各数
，0.31，
，
，
，0.90108，
中，无理数有（ ）
| 3 |
| ||
| 2 |
| π |
| 3 |
| 1 |
| 7 |
6+
|
| A、2个 | B、3个 | C、4个 | D、5个 |
方程x（x-5）=0的根是（ ）
| A、x=0 |
| B、x=5 |
| C、x1=0，x2=5 |
| D、x1=0，x2=-5 |
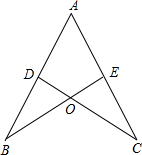如图，AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．