题目内容
如图，已知PA是⊙O的切线，切点为A，PO=2，∠APO=30°，那么⊙O的半径是（ ）| A、2 | B、1 | C、3 | D、4 |
考点：切线的性质
专题：几何图形问题
分析：连接OA，根据切线的性质得到直角三角形，在直角三角形中求出半径的长．
解答：
解：如图：连接OA，
∵PA是⊙O的切线，切点为A，
∴OA⊥PA
在直角△OAP中，
PO=2，∠APO=30°，
∴OA=PO×sin∠P=1．
故选B．
解：如图：连接OA，∵PA是⊙O的切线，切点为A，
∴OA⊥PA
在直角△OAP中，
PO=2，∠APO=30°，
∴OA=PO×sin∠P=1．
故选B．
点评：本题考查的是切线的性质，利用切线的性质得到直角三角形，求出线段的长．
练习册系列答案
阅读快车系列答案
相关题目
下列说法中正确的是（ ）
| A、-an和（-a）n一定是互为相反数 |
| B、当n为奇数时，-an和（-a）n相等 |
| C、当n为偶数时，-an和（-a）n相等 |
| D、-an和（-a）n一定不相等 |
若
+|x-y-3|=0，则x+y的算术平方根为（ ）
| x-2y+9 |
A、±3
| ||
| B、3 | ||
C、3
| ||
| D、27 |
下列语句中是命题的是（ ）
| A、∠A=50° |
| B、作直线⊥ab |
| C、对顶角相等吗？ |
| D、延长AB到C使BC=2AB |
下列各组数中，可以构成直角三角形的一组是（ ）
| A、2，5，6 |
| B、2，3，4 |
| C、6，7，9 |
| D、15，20，25 |
已知a＜0，则点P（a2，-a+1）关于原点的对称点P′在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列两点都在一次函数y=-2x+3的图象上的是（ ）
| A、原点和点（1，1） |
| B、（1，1）和（2，3） |
| C、（0，3）和（1，1） |
| D、（0，3）和（2，3） |
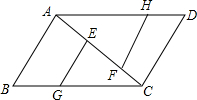如图，E、F是?ABCD的对角线AC上的两点，且AF=CE．G、H是?ABCD的边BC、AD上的两点且BG=DH，请你猜想线段GE与HF之间的关系，并加以证明．