题目内容
20.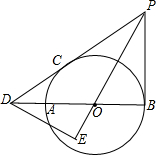 如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.
如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径.
分析 (1)由切线长定理,知∠DPO=∠BPO,在△EOD和△BOP中,根据等角的余角相等,得∠BPO=∠EDB,从而问题得证.
(2)在Rt△PBD中由勾股定理易得PD的长、由切线长定理知PB=PC,可计算出CD的长;若设圆的半径为r,OD=4-r,OC=r,在Rt△DCO中,根据勾股定理得到关于r的方程,求出⊙O的半径.
解答  (1)证明:∵PC、PB是⊙O的切线,
(1)证明:∵PC、PB是⊙O的切线,
∴∠DPO=∠OPB,
∵DE⊥PO,∴∠E=90°,
∵点B是切点,PB是切线
所以∠PBD=90°,
∴∠E=∠PBD,又∵∠POB=∠EOD
∴∠EDB=∠OPB
∴∠DPO=∠EDB
(2)解:连接OC,
∵PC、PB是⊙O的切线,切点为B、C,
∴PB=PC,∠PCO=90°.
在Rt△PBD中,∵PB=3,DB=4,∴PD=5,
∴DC=PD-PC=2
设⊙O半径为r,则OD=BD-r=4-r
在Rt△DCO中,r2+22=(4-r)2
∴r=1.5
即⊙O的半径为1.5.
点评 本题考查了勾股定理,切线长定理、切线的性质及一元二次方程的解法.解决本题(1)的关键是利用切线长定理得到∠DPO=∠OPB,由同角的余角相等得到∠BPO=∠EDB;解决(2)的关键是利用勾股定理得到关于半径的方程.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
12.如a>b,那么下列不等式中正确的是( )
| A. | -$\frac{a}{2}$>-$\frac{b}{2}$ | B. | 2-a<2-b | C. | ac2>bc2 | D. | b-a>0 |
9.下列选项正确的是( )
| A. | $\sqrt{1}$=±1 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\root{3}{-125}$=-5 | D. | $\sqrt{-1}$=1 |
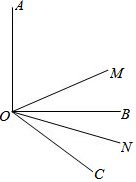 (1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.
(1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.