题目内容
17. 线段AB、CD交于O,若AB=CD,且AB⊥CD,求证:AC+BD>$\sqrt{2}$AB.
线段AB、CD交于O,若AB=CD,且AB⊥CD,求证:AC+BD>$\sqrt{2}$AB.
分析 作?ABEC,连接DE,得到AC=BE,AB=CE=CD,由AB⊥CD,AB∥CE,得到△CED是等腰直角三角形,根据勾股定理求得DE=$\sqrt{2}CD$=$\sqrt{2}$AB,由三角形的三边关系得到结论.
解答  解:如图作?ABEC,连接DE,
解:如图作?ABEC,连接DE,
∴AC=BE,
∴AB=CE=CD,
∵AB⊥CD,AB∥CE,
∴∠ECD=90°
∴△CED是等腰直角三角形,
∴DE=$\sqrt{2}CD$=$\sqrt{2}$AB,
在△BED中,BE+BD=AC+BD>DE,
∴AC+BD>$\sqrt{2}$AB.
点评 本题考查了平行四边形的性质和判定,等腰直角三角形的性质,三角形的三边关系,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.在锐角△ABC中,cosA=$\frac{3}{5}$,cosB=$\frac{12}{13}$,BC=13,则△ABC的面积为( )
| A. | $\frac{65}{2}$ | B. | 30 | C. | 78 | D. | $\frac{315}{8}$ |
 实数a、b在数轴上的位置如图所示,则$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$=2b.
实数a、b在数轴上的位置如图所示,则$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$=2b.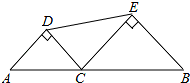 如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么AC为多长时DE的长最小?最小值为多少?
如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么AC为多长时DE的长最小?最小值为多少?