题目内容
16.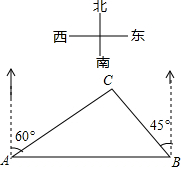 如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).
如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).
分析 作CD⊥AB于点D,在Rt△ACD中利用三角函数求得CD的长,然后在Rt△BCD中求得BC的长,然后根据$\frac{v_1}{v_2}$=$\frac{BC}{AC}$求解.
解答  解:作CD⊥AB于点B.
解:作CD⊥AB于点B.
∵在Rt△ACD中,∠CAD=90°-60°=30°,
∴CD=AC•sin∠CAD=4×$\frac{1}{2}$=2(km),
∵Rt△BCD中,∠CBD=90°,
∴BC=$\sqrt{2}$CD=2$\sqrt{2}$(km),
∴$\frac{v_1}{v_2}$=$\frac{AC}{BC}$=$\frac{4}{2\sqrt{2}}$=$\sqrt{2}$.
故答案是:$\sqrt{2}$.
点评 本题考查了解直角三角形的应用,作出辅助线,转化为直角三角形的计算,求得BC的长是关键.

练习册系列答案
相关题目
7.函数y=$\frac{x}{2-x}$中自变量x的取值范围是( )
| A. | x≠2 | B. | x≥2 | C. | x≤2 | D. | x>2 |
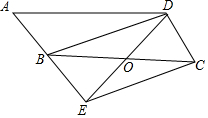 如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.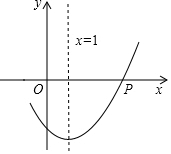 如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为(-2,0).
如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为(-2,0).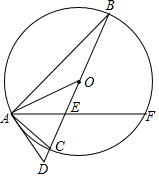 如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.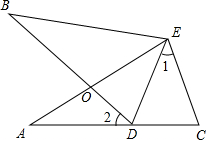 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.