题目内容
6.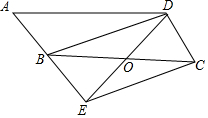 如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.
分析 (1)由AAS证明△BOE≌△COD,得出OE=OD,即可得出结论;
(2)由平行四边形的性质得出∠BCD=∠A=50°,由三角形的外角性质求出∠ODC=∠BCD,得出OC=OD,证出DE=BC,即可得出结论.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,$\left\{\begin{array}{l}{∠OEB=∠ODC}\\{∠BOE=∠COD}\\{BO=CO}\end{array}\right.$,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:若∠A=50°,则当∠BOD=100°时,四边形BECD是矩形.理由如下:
∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=100°-50°=50°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;
故答案为:100.
点评 此题主要考查了矩形的判定、平行四边形的判定与性质、全等三角形的判定与性质等知识;熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
11.已知点(-1,y1),(4,y2)在一次函数y=3x-2的图象上,则y1,y2,0的大小关系是( )
| A. | 0<y1<y2 | B. | y1<0<y2 | C. | y1<y2<0 | D. | y2<0<y1 |
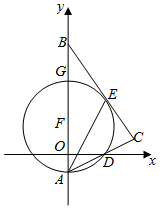 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.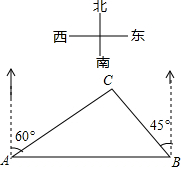 如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).
如图,在一笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头 A北偏东60°的方向,在码头 B北偏西45°的方向,AC=4km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A、B的游船速度分别为v1、v2,若回到 A、B所用时间相等,则$\frac{v_1}{v_2}$=$\sqrt{2}$(结果保留根号).