题目内容
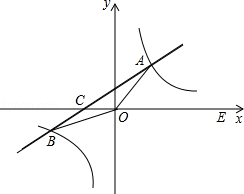 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函y=| m |
| x |
| 3 |
| 4 |
(1)求反比例函数解析式;
(2)求△AOB的面积;
(3)求不等式kx+b≥
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)首先过点A作AD⊥x轴,由线段OA=5,E为x轴正半轴上一点,且tan∠AOC=
,可求得点A的坐标,然后利用待定系数法求得反比例函数的解析式;
(2)把点B的坐标(-6,n)代入y=
得,确定出点B的坐标,根据A、B的坐标利用待系数法即可求得直线AB的解析式,进而求得C的坐标,根据S△AOB=S△AOC+S△BOC即可求出三角形AOB的面积;
(2)观察图象,即可求得一次函数值大于反比例函数值时x的取值范围,即不等式kx+b≥
的解集.
| 3 |
| 4 |
(2)把点B的坐标(-6,n)代入y=
| 12 |
| x |
(2)观察图象,即可求得一次函数值大于反比例函数值时x的取值范围,即不等式kx+b≥
| m |
| x |
解答: 解:(1)过点A作AD⊥x轴,
解:(1)过点A作AD⊥x轴,
∵在Rt△AOD中,tan∠AOE=
=
,
设AD=3x,OD=4x,
∵OA=5,
在Rt△AOD中,根据勾股定理解得AD=3,OD=4,
∴A(4,3),
把A(4,3)代入反比例函数y=
中,
解得:m=12,
则反比例函数的解析式为y=
;
(2)点B的坐标(-6,n)代入y=
得:n=-2,
∴B(-6,-2),
∵一次函数y=kx+b(k≠0)的图象与反比例函y=
的图象交于第一、第三象限内的A、B两点,
∴
,解得
∴一次函数的解析式是y=
x+1;
∴C(-2,0),
∴S△AOB=S△AOC+S△BOC=
×2×3+
×2×2=5;
(2)如图,一次函数值大于反比例函数值时x的取值范围为:-6≤x<0或x≥4.
即不等式kx+b≥
的解集为:-6≤x<0或x≥4.
 解:(1)过点A作AD⊥x轴,
解:(1)过点A作AD⊥x轴,∵在Rt△AOD中,tan∠AOE=
| AD |
| OD |
| 3 |
| 4 |
设AD=3x,OD=4x,
∵OA=5,
在Rt△AOD中,根据勾股定理解得AD=3,OD=4,
∴A(4,3),
把A(4,3)代入反比例函数y=
| m |
| x |
解得:m=12,
则反比例函数的解析式为y=
| 12 |
| x |
(2)点B的坐标(-6,n)代入y=
| 12 |
| x |
∴B(-6,-2),
∵一次函数y=kx+b(k≠0)的图象与反比例函y=
| m |
| x |
∴
|
|
∴一次函数的解析式是y=
| 1 |
| 2 |
∴C(-2,0),
∴S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图,一次函数值大于反比例函数值时x的取值范围为:-6≤x<0或x≥4.
即不等式kx+b≥
| m |
| x |
点评:此题考查了反比例函数与一次函数的交点问题.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示的滑雪人经过旋转或平移不能得到的是( )
如图所示的滑雪人经过旋转或平移不能得到的是( )A、 |
B、 |
C、 |
D、 |
在平面直角坐标系中,点P(3,1)所在象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
抛一枚质地均匀的骰子,向上一面的点数大于2且小于5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.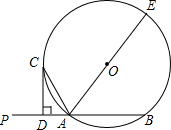 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D. 如图,已知矩形ABCD,BC在x轴上,AB=2,BC=3,点A的坐标为(-1,2),过原点的直线平分矩形ABCD的面积,则此直线的解析式为
如图,已知矩形ABCD,BC在x轴上,AB=2,BC=3,点A的坐标为(-1,2),过原点的直线平分矩形ABCD的面积,则此直线的解析式为