题目内容
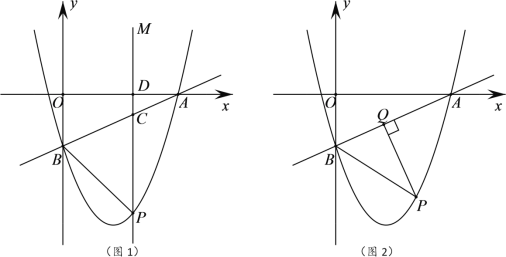
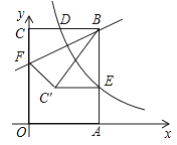
【题目】以矩形![]() 的顶点
的顶点![]() 为坐标原点建立平面直角坐标系,使点
为坐标原点建立平面直角坐标系,使点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,双曲线
轴的正半轴上,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,且与
,且与![]() 交于点
交于点![]() ,过
,过![]() 边上一点
边上一点![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在矩形内部的一点
落在矩形内部的一点![]() 处,且
处,且![]() ,若点
,若点![]() 的坐标为(2,4),则
的坐标为(2,4),则![]() 的值为______.
的值为______.
【答案】![]()
【解析】
延长E![]() 交OC于点G,设点D的坐标为(a,
交OC于点G,设点D的坐标为(a,![]() ),根据矩形的性质和反比例函数的特征即可证出点E为AB的中点,然后根据点
),根据矩形的性质和反比例函数的特征即可证出点E为AB的中点,然后根据点![]() 的坐标和折叠的性质即可各线段之间的关系,最后利用勾股定理列出方程即可求出CF和BC,最后根据正切的定义计算即可.
的坐标和折叠的性质即可各线段之间的关系,最后利用勾股定理列出方程即可求出CF和BC,最后根据正切的定义计算即可.
解:延长E![]() 交OC于点G
交OC于点G
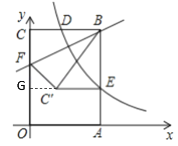
∵四边形OABC为矩形,双曲线![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,设点D的坐标为(a,
,设点D的坐标为(a,![]() )
)
∴点B的坐标为(2a,![]() ),即BC=2a
),即BC=2a
∴点E的坐标为(2a,![]() ),EG=BC=2a
),EG=BC=2a
∴点E为AB的中点
∵![]() ,若点
,若点![]() 的坐标为(2,4),
的坐标为(2,4),
∴OG=AE=BE=4,OC=AB=2AE=8,![]()
由折叠性质可知:CF=![]() F,B
F,B![]() =BC=2a
=BC=2a
∴FG=OC-OG-CF=4-CF,![]() E=EG-
E=EG-![]() =2a-2
=2a-2
根据勾股定理可得:FG2+![]() 2=
2=![]() F2,
F2,![]() E 2+BE 2= B
E 2+BE 2= B![]() 2,
2,
即(4-CF)2+22= CF 2,(2a-2) 2+4 2= (2a)2,
解得:CF=![]() ,a=
,a=![]()
∴BC=2×![]() =5
=5
∴![]() =
=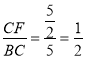
故答案为:![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目