题目内容
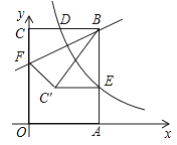
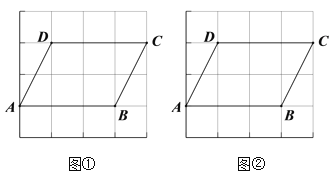
【题目】如图,正方形![]() 的边
的边![]() ,
,![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,规定点
轴的正方向运动,规定点![]() 到达点
到达点![]() 时,点
时,点![]() 停止运动,点
停止运动,点![]() 也停止运动.连接
也停止运动.连接![]() ,过点
,过点![]() 作
作![]() 的垂线,与过点
的垂线,与过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 相交于点D,
相交于点D,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() .
.
(1)求![]() 的度数及点
的度数及点![]() 的坐标(用
的坐标(用![]() 表示).
表示).
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)探索![]() 周长是否随时间
周长是否随时间![]() 的变化而变化.若变化,说明理由;若不变,试求出这个定值.
的变化而变化.若变化,说明理由;若不变,试求出这个定值.
【答案】(1)![]() (2)当
(2)当![]() 为4秒或
为4秒或![]() 秒时,
秒时,![]() 为等腰三角形(3)周长是定值,该定值为8
为等腰三角形(3)周长是定值,该定值为8
【解析】
(1)易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标.
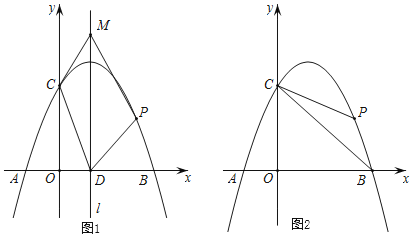
(2)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.由于△PBE底边不定,故分三种情况讨论,借助于三角形全等及勾股定理进行求解,然后结合条件进行取舍,最终确定符合要求的t值.
(3)由(2)已证的结论EP=AP+CE很容易得到△POE周长等于AO+CO=8,从而解决问题.
(1)
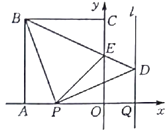
如图①.由题可得![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,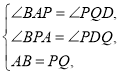
![]() .
.![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.![]() 点
点![]() 坐标为
坐标为![]() .
.
(2)①若![]() ,则
,则![]() .
.![]() .
.
![]() ,
,![]() .
.
![]() 点
点![]() 与点
与点![]() 重合.
重合.
![]() 点
点![]() 与点
与点![]() 重合.与条件“
重合.与条件“![]() 轴”矛盾,
轴”矛盾,
![]() 这种情况应舍去.
这种情况应舍去.
②若![]() ,则
,则![]() .
.![]() .
.
![]() .
.
在![]() 和
和![]() 中,
中,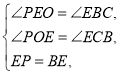
![]() ≌
≌![]() .
.![]() ,
,![]() .
.![]() .
.
![]() 点
点![]() 与点
与点![]() 重合(
重合(![]() ).
).![]() 点
点![]() 与点
与点![]() 重合(
重合(![]() ).
).
![]() 点
点![]() ,
,![]() .此时
.此时![]() .
.
③若![]() ,
,
在![]() 和
和![]() 中,
中,![]()
![]() .
.
![]() .
.![]() ,
,![]() .
.![]() .
.
![]() ,
,![]() .
.
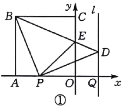
延长![]() 到点
到点![]() ,使得
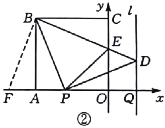
,使得![]() ,连接
,连接![]() ,如图②所示.
,如图②所示.
在![]() 和
和![]() 中,
中,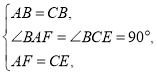
![]() .
.![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() .
.![]() .
.
在![]() 和
和![]() 中,
中,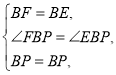
![]() .
.
![]() .
.![]() .
.
![]() .
.
![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 为4秒或
为4秒或![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.
(3)![]() ,
,
![]() .
.
![]() 周长是定值,该定值为8.
周长是定值,该定值为8.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目