题目内容
2.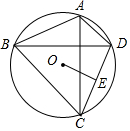 如图,圆O中,弦AC⊥BD,且OE⊥CD于E,若AB的长是10,则OE的长是5.
如图,圆O中,弦AC⊥BD,且OE⊥CD于E,若AB的长是10,则OE的长是5.
分析 作直径DF,连接BF,CF,则∠DCF=90°,∠1+∠2=90°,由圆周角定理得出∠2=∠4,故可得出∠1=∠3,由此得出CF的长,根据三角形中位线定理即可得出结论.
解答 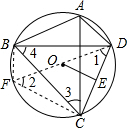 解:作直径DF,连接BF,CF,则∠DCF=90°,∠1+∠2=90°,
解:作直径DF,连接BF,CF,则∠DCF=90°,∠1+∠2=90°,
∵AC⊥BD,
∴∠3+∠4=90°.
∵∠2=∠4,
∴∠1=∠3,
∴$\widehat{AB}$=$\widehat{CF}$,
∴AB=CF=10.
∴OE⊥CD于点E,
∴CE=DE.
∵OD=OF,
∴OE=$\frac{1}{2}$CF=5.
故答案为:5.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,⊙O是△ABC的外接圆,∠BAC=60°,AD为⊙O的直径,AD交BC点E,CE=2,BE=4
如图,⊙O是△ABC的外接圆,∠BAC=60°,AD为⊙O的直径,AD交BC点E,CE=2,BE=4 如图,四边形ABCD和AEFG均为正方形,则DG:CF:BE=1:$\sqrt{2}$:1.
如图,四边形ABCD和AEFG均为正方形,则DG:CF:BE=1:$\sqrt{2}$:1. 如图,直线y=x+t和抛物线y=x2+bx+c相交于A(1,0),B(4,3)两点,则t的值为-1,不等式x2+(b-1)x+c-t>0的解集为x<1或x>4.
如图,直线y=x+t和抛物线y=x2+bx+c相交于A(1,0),B(4,3)两点,则t的值为-1,不等式x2+(b-1)x+c-t>0的解集为x<1或x>4.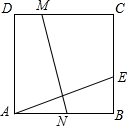 如图所示,四边形ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边形BCMN的面积和四边形ADMN的面积分别为S1,S2.求S1:S2.
如图所示,四边形ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边形BCMN的面积和四边形ADMN的面积分别为S1,S2.求S1:S2.