题目内容
3.已知某抛物线是由y=-$\frac{1}{2}$x2沿y轴向上平移得到的,且知道它经过点(2,3).(1)求这条抛物线的表达式,并写出顶点P的坐标;
(2)若这条抛物线与x轴交于点A、B,试求△PAB的面积.
分析 (1)抛物线的顶点坐标为(0,0),再利用点平移的坐标规律,把点(0,0)向上平移m个单位所得对应点的坐标为(0,m),则根据顶点式写出平移的抛物线解析式为y=x2+m,然后把点(2,3)代入求出m的值即可得到平移后得到的抛物线的解析式.
(2)由抛物线的解析式求得A、B的坐标,进而根据三角形面积公式即可求得.
解答 解:(1)y=-$\frac{1}{2}$x2,
∴抛物线的顶点坐标为(0,0),点(0,0)向上平移m个单位所得对应点的坐标为(0,m),
∴平移的抛物线解析式为y=-$\frac{1}{2}$x2+m,把点(2,3)代入得
-2+m=3,解得m=5,
∴平移后的抛物线解析式为y=-$\frac{1}{2}$x2+5.
∴顶点P的坐标为(0,5).
(2)令y=0,则-$\frac{1}{2}$x2+5=0,
解得x=±$\sqrt{10}$,
∴A(-$\sqrt{10}$,0),B($\sqrt{10}$,0),
∴AB=2$\sqrt{10}$,
∴△PAB的面积=$\frac{1}{2}$×2$\sqrt{10}$×5=5$\sqrt{10}$.
点评 本题考查了二次函数图象与几何变换以及抛物线与x轴的交点,求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
 如图,直线y=x+t和抛物线y=x2+bx+c相交于A(1,0),B(4,3)两点,则t的值为-1,不等式x2+(b-1)x+c-t>0的解集为x<1或x>4.
如图,直线y=x+t和抛物线y=x2+bx+c相交于A(1,0),B(4,3)两点,则t的值为-1,不等式x2+(b-1)x+c-t>0的解集为x<1或x>4. 如图,△ABC内接于⊙O,∠C=30°,AB=4,连结OA,OB,则扇形OAB的面积为$\frac{8}{3}$π.
如图,△ABC内接于⊙O,∠C=30°,AB=4,连结OA,OB,则扇形OAB的面积为$\frac{8}{3}$π.

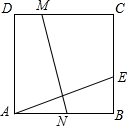 如图所示,四边形ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边形BCMN的面积和四边形ADMN的面积分别为S1,S2.求S1:S2.
如图所示,四边形ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边形BCMN的面积和四边形ADMN的面积分别为S1,S2.求S1:S2.