题目内容
计算:(2+1)(22+1)(24+1)(28+1)(216+1)…(22n+1).
考点:平方差公式
专题:计算题
分析:原式变形后,利用平方差公式计算即可得到结果.
解答:解:原式=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)…(22n+1)
=(22-1)(22+1)(24+1)(28+1)(216+1)…(22n+1)
=(24-1)(24+1)(28+1)(216+1)…(22n+1)
=(28-1)(28+1)(216+1)…(22n+1)
=(216-1)(216+1)…(22n+1)
=…
=24n-1.
=(22-1)(22+1)(24+1)(28+1)(216+1)…(22n+1)
=(24-1)(24+1)(28+1)(216+1)…(22n+1)
=(28-1)(28+1)(216+1)…(22n+1)
=(216-1)(216+1)…(22n+1)
=…
=24n-1.
点评:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目

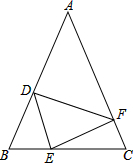 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE. 平行四边形ABCD的周长为40,高AE=6,高AF=9.
平行四边形ABCD的周长为40,高AE=6,高AF=9. 如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=8cm,DC=3cm,则AE=
如图,AD=BD,AD⊥BC,垂足为D,BF⊥AC,垂足为F,BC=8cm,DC=3cm,则AE=