题目内容
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形:
(1)∠A=30°,BC=2
(2)AB=10,AC=5.
(1)∠A=30°,BC=2
(2)AB=10,AC=5.
考点:解直角三角形
专题:
分析:(1)根据∠A=30°可以求得∠B的值,再根据BC=2和tan30°的值可求得AC的值,根据30°角所对直角边是斜边一半即可求得AB的长,即可解题;
(2)根据AB和AC的值可以求得BC的值,再根据sinA即可求得∠A的度数,进而得到∠B的值.
(2)根据AB和AC的值可以求得BC的值,再根据sinA即可求得∠A的度数,进而得到∠B的值.
解答:解:(1)∵∠C=90°,∠A=30°,
∴∠B=60°,
∵BC=2,tanA=tan30°=
,
∴AC=2
,
∵∠A=30°,BC=2,
∴AB=4;
(2)∵AB=10,AC=5,
∴BC=
=5
,
∵AB=2AC,
∴sinA=
,
∴∠B=30°,
∴∠A=60°.
∴∠B=60°,
∵BC=2,tanA=tan30°=
| ||
| 3 |
∴AC=2
| 3 |
∵∠A=30°,BC=2,
∴AB=4;
(2)∵AB=10,AC=5,
∴BC=
| AB2-AC2 |
| 3 |
∵AB=2AC,
∴sinA=
| 1 |
| 2 |
∴∠B=30°,
∴∠A=60°.
点评:本题考查了直角三角形中三角函数值的运用,考查了勾股定理的运用,考查了特殊角的三角函数值,本题中根据30°角所对直角边是斜边一半的性质解题是解题的关键.

练习册系列答案
相关题目
 如图所示,在正方形ABCD中,若对角线长为10cm,则PE+PF=
如图所示,在正方形ABCD中,若对角线长为10cm,则PE+PF=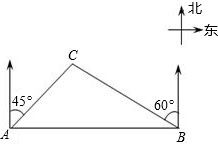 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图所示,在A地北偏东45°、B地北偏西60°方向上有一牧民区C.求牧民区C到B地的距离.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图所示,在A地北偏东45°、B地北偏西60°方向上有一牧民区C.求牧民区C到B地的距离. 如图,AB=AC,AB是圆的直径,AC,BC和圆交于点D,E,连接BE
如图,AB=AC,AB是圆的直径,AC,BC和圆交于点D,E,连接BE