题目内容
 平行四边形ABCD的周长为40,高AE=6,高AF=9.
平行四边形ABCD的周长为40,高AE=6,高AF=9.(1)求AB,BC的长;
(2)?ABCD的面积.
考点:平行四边形的性质
专题:
分析:(1)根据平行四边形的性质得出AB=DC,AD=BC,求出BC+DC=20,根据面积求出6BC=9DC,求出即可;
(2)根据面积公式求出即可.
(2)根据面积公式求出即可.
解答:解:(1)∵S平行四边形ABCD=BC×AE=DC×AF,
∴6BC=9DC,
∵平行四边形ABCD的周长为40,
∴BC+DC=20,
即
解得:DC=8,BC=12,
即AB=DC=8,BC=12;
(2)?ABCD的面积为BC×AE=12×6=72.
∴6BC=9DC,
∵平行四边形ABCD的周长为40,
∴BC+DC=20,
即
|
解得:DC=8,BC=12,
即AB=DC=8,BC=12;
(2)?ABCD的面积为BC×AE=12×6=72.
点评:本题考查了平行四边形的性质的应用,注意:平行四边形的对边相等,平行四边形的面积等于底乘以高.

练习册系列答案
相关题目
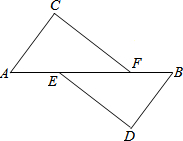 如图:A、E、F、B在一条直线上,下面四个条件:①AC=BD;②AE=BF;③AC∥BD;④∠C=∠D,请用其中三个作为条件,余下的一个作为结论,编一道数学问题,并写出解答过程.
如图:A、E、F、B在一条直线上,下面四个条件:①AC=BD;②AE=BF;③AC∥BD;④∠C=∠D,请用其中三个作为条件,余下的一个作为结论,编一道数学问题,并写出解答过程.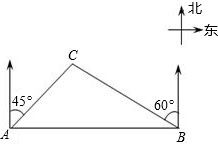 某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图所示,在A地北偏东45°、B地北偏西60°方向上有一牧民区C.求牧民区C到B地的距离.
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图所示,在A地北偏东45°、B地北偏西60°方向上有一牧民区C.求牧民区C到B地的距离.