题目内容
6. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )| A. | m=5 | B. | m=4$\sqrt{5}$ | C. | m=3$\sqrt{5}$ | D. | m=10 |
分析 先根据平行四边形的性质求出△OCD∽△OEB,再根据相似三角形的性质解答即可.
解答 解:∵AB∥CD,
∴△OCD∽△OEB,
又∵E是AB的中点,
∴2EB=AB=CD,
∴$\frac{{S}_{△OEB}}{{S}_{△OCD}}$=($\frac{BE}{CD}$)2,即$\frac{\sqrt{5}}{m}=(\frac{1}{2})^{2}$,
解得m=4$\sqrt{5}$,
故选B.
点评 本题考查的是相似三角形的判定与性质,涉及到平行四边形的性质等知识,熟练掌握相似三角形的判定和性质是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
17.已知sinα=$\frac{\sqrt{3}}{2}$,则锐角α的度数是( )
| A. | 30° | B. | 37° | C. | 45° | D. | 60° |
1.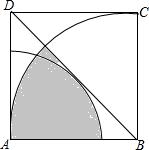 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{π}{2}-1$ | C. | $\frac{5π}{4}-1$ | D. | $\frac{3π}{4}-1$ |
11.若二次根式$\sqrt{x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤1 | D. | x≥1 |
18.四个数-3,0,1,2,其中负数是( )
| A. | -3 | B. | 0 | C. | 1 | D. | 2 |
15.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
16.若分式$\frac{x-2}{x+5}$的值为0,则x的值是( )
| A. | x=2 | B. | x=-2 | C. | x=-5 | D. | x=0 |
 如图,AB是⊙O的直径,弦CD⊥AB于点C,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2.AF=3.给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点C,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2.AF=3.给出下列结论: