题目内容
15.已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是( )| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
分析 根据圆心距和两圆半径的关系即可求解.
解答 解:∵两圆的半径分别为2和3,圆心距为5,
而3+2=5,
∴d=R+r,
∴这两圆的位置关系是外切.
故选B.
点评 本题考查了由数量关系来判断两圆位置关系的方法.圆和圆的位置与两圆的圆心距、半径的数量之间的关系(设两圆的半径分别为R和r,且R≥r,圆心距为d)为:
①两圆外离?d>R+r;
②两圆外切?d=R+r;
③两圆相交?R-r<d<R+r;
④两圆内切?d=R-r;
⑤两圆内含?d<R-r.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
6. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )| A. | m=5 | B. | m=4$\sqrt{5}$ | C. | m=3$\sqrt{5}$ | D. | m=10 |
3.小军同学在学校组织的社会实践活动中,负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表:
(1)请根据题中已有的信息补全频数分布:①15,②6,③12%;
(2)如果家庭月均用水量在5≤x<8范围内为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)记月均用水量在2≤x<3范围内的两户为a1,a2,在7≤x<8范围内的3户b1、b2、b3,从这5户家庭中任意抽取2户,试完成下表,并求出抽取出的2户家庭来自不同范围的概率.
| 月均用水量 | 2≤x<3 | 3≤x<4 | 4≤x<5 | 5≤x<6 | 6≤x<7 | 7≤x<8 | 8≤x<9 |
| 频数 | 2 | 12 | ① | 10 | ② | 3 | 2 |
| 百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
(2)如果家庭月均用水量在5≤x<8范围内为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)记月均用水量在2≤x<3范围内的两户为a1,a2,在7≤x<8范围内的3户b1、b2、b3,从这5户家庭中任意抽取2户,试完成下表,并求出抽取出的2户家庭来自不同范围的概率.
| a1 | a2 | b1 | b2 | b3 | |
| a1 | |||||
| a2 | |||||
| b1 | |||||
| b2 | |||||
| b3 |
10.计算3x3•(-2x2)的结果是( )
| A. | -6x5 | B. | -6x6 | C. | -x5 | D. | x5 |
20.实数-2016的相反数是( )
| A. | 2016 | B. | -2016 | C. | ±2016 | D. | $\frac{1}{2016}$ |
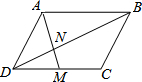 如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于( )
如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于( ) 小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)
小明上学途中要经过A,B两地,由于A,B两地之间有一片草坪,所以需要走路线AC,CB,如图,在△ABC中,AB=63m,∠A=45°,∠B=37°,求AC,CB的长.(结果保留小数点后一位)