题目内容
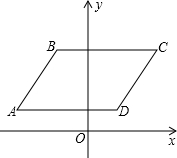 如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(-5,1),B(-2,4),C(5,4),点D在第一象限.
如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(-5,1),B(-2,4),C(5,4),点D在第一象限.(1)写出D点的坐标;
(2)求经过B、D两点的直线的解析式,并求线段BD的长;
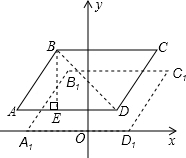
(3)将平行四边形ABCD先向右平移1个单位长度,再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.
考点:一次函数综合题
专题:压轴题,待定系数法
分析:(1)根据点B、C的坐标求出BC的长度,再根据平行四边形的对边相等列式求出点D的横坐标,然后写出D点坐标即可;
(2)设直线BD的解析式为y=kx+b,然后利用待定系数法求一次函数解析式解答;过点B作BE⊥AD于E,求出BE、DE的长,然后利用勾股定理列式计算即可得解;
(3)根据向右平移横坐标加,向下平移纵坐标减求出A1、B1、C1、D1的坐标,然后求出重叠部分平行四边形的底边和高,再根据平行四边形的面积公式列式计算即可得解.
(2)设直线BD的解析式为y=kx+b,然后利用待定系数法求一次函数解析式解答;过点B作BE⊥AD于E,求出BE、DE的长,然后利用勾股定理列式计算即可得解;
(3)根据向右平移横坐标加,向下平移纵坐标减求出A1、B1、C1、D1的坐标,然后求出重叠部分平行四边形的底边和高,再根据平行四边形的面积公式列式计算即可得解.
解答:解:(1)∵B(-2,4),C(5,4),
∴BC=5-(-2)=5+2=7,
∵A(-5,1),
∴点D的横坐标为-5+7=2,
∴点D的坐标为(2,1);
(2)设直线BD的解析式为y=kx+b,
将B(-2,4)、D(2,1)代入得:
,
解得
,
∴经过B、D两点的直线的解析式为y=-
x+
,
过B点作AD的垂线,垂足为E,则BE=4-1=3,
DE=2-(-2)=2+2=4,
在Rt△BDE中,BD=
=
=5;
(3)∵?ABCD向右平移1个单位长度,再向下平移1个单位长度,
∴A1(-4,0),B1(-1,3),C1(6,3)D1(3,0),
∴重叠部分的底边长7-1=6,
高为3-1=2,
∴重叠部分的面积S=6×2=12.
∴BC=5-(-2)=5+2=7,
∵A(-5,1),
∴点D的横坐标为-5+7=2,
∴点D的坐标为(2,1);
(2)设直线BD的解析式为y=kx+b,
将B(-2,4)、D(2,1)代入得:
|

解得
|
∴经过B、D两点的直线的解析式为y=-
| 3 |
| 4 |
| 5 |
| 2 |
过B点作AD的垂线,垂足为E,则BE=4-1=3,
DE=2-(-2)=2+2=4,
在Rt△BDE中,BD=
| BE2+DE2 |
| 32+42 |
(3)∵?ABCD向右平移1个单位长度,再向下平移1个单位长度,
∴A1(-4,0),B1(-1,3),C1(6,3)D1(3,0),
∴重叠部分的底边长7-1=6,
高为3-1=2,
∴重叠部分的面积S=6×2=12.
点评:本题是一次函数综合题型,主要利用了平行四边形的性质,待定系数法求一次函数解析式,勾股定理的应用,难点在于(3)判断出重叠部分是平行四边形并且求出底边和高的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若分式方程
=2的一个解是x=1,则a=( )
| x+1 |
| x+a |
| A、0 | B、1 | C、2 | D、-1 |
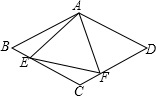 如图,在菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数.
如图,在菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数. 如图,根据要求画图(保留画图的痕迹,可以不写结论).
如图,根据要求画图(保留画图的痕迹,可以不写结论).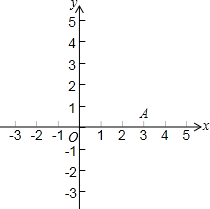 如图,已知抛物线y=-x2+mx+3与x轴的一个交点A(3,0).
如图,已知抛物线y=-x2+mx+3与x轴的一个交点A(3,0).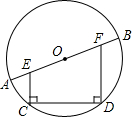 如图,在⊙O中,CD为弦,EC⊥CD,FD⊥CD,EC,FD分别交直径AB于E,F两点.
如图,在⊙O中,CD为弦,EC⊥CD,FD⊥CD,EC,FD分别交直径AB于E,F两点.