题目内容
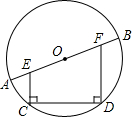 如图,在⊙O中,CD为弦,EC⊥CD,FD⊥CD,EC,FD分别交直径AB于E,F两点.
如图,在⊙O中,CD为弦,EC⊥CD,FD⊥CD,EC,FD分别交直径AB于E,F两点.(1)求证:AE=BF;
(2)当弦CD与直径AB相交时,其他条件不变,结论成立吗?试另画出图形,不用证明;
(3)若把条件EC⊥CD,FD⊥CD改成AE⊥CD,BF⊥CD,AE,BF分别交CD于E,F两点,则结论会有什么变化?试另画图并加以证明.
考点:垂径定理,梯形中位线定理
专题:几何图形问题,探究型
分析:(1)过点O作OH⊥CD,根据垂径定理得到CH=DH,由于FD⊥CD,EC⊥CD,所以CE∥OH∥DF,于是可判断OH为梯形CDFE的中位线,则OE=OF,然后利用等量减等量差相等即可得到结论;
(2)当弦CD与直径AB相交时,根据叙述即可作出图形,与(1)的方法相同,即可写出结论;
(3)作OM⊥CD,根据垂径定理和平行线分线段成比例定理即可证得.
(2)当弦CD与直径AB相交时,根据叙述即可作出图形,与(1)的方法相同,即可写出结论;
(3)作OM⊥CD,根据垂径定理和平行线分线段成比例定理即可证得.
解答:(1)证明:过点O作OH⊥CD,如图1,
则CH=DH,
∵FD⊥CD,EC⊥CD,
∴CE∥OH∥DF,
∴OH为梯形CDFE的中位线,
∴点O为EF的中点,即OE=OF,
而OA=OB,
∴OA-OE=OB-OF,
即AE=BF;
(2)AE=DF.图形如2.
;
(3)如图3.结论:EC=DF.
证明:作OM⊥CD,则CM=DM.
∵AE⊥CD,BF⊥CD,
∴AE∥OM∥BF,
又∵OA=OB,
∴EM=FM,
∴EC=DF.

则CH=DH,
∵FD⊥CD,EC⊥CD,
∴CE∥OH∥DF,
∴OH为梯形CDFE的中位线,
∴点O为EF的中点,即OE=OF,
而OA=OB,
∴OA-OE=OB-OF,
即AE=BF;
(2)AE=DF.图形如2.
;

(3)如图3.结论:EC=DF.

证明:作OM⊥CD,则CM=DM.
∵AE⊥CD,BF⊥CD,
∴AE∥OM∥BF,
又∵OA=OB,
∴EM=FM,
∴EC=DF.
点评:本题考查了垂径定理和平行线分线段成比例定理,正确作出辅助线是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
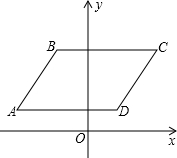 如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(-5,1),B(-2,4),C(5,4),点D在第一象限.
如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(-5,1),B(-2,4),C(5,4),点D在第一象限.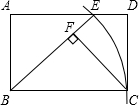 如图,在矩形ABCD中,以顶点B为圆心、边BC长为半径作弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,以顶点B为圆心、边BC长为半径作弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.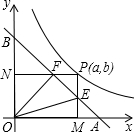 如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴正半轴分别交于点A和点B,且OA=OB=1.这条曲线是函数
如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴正半轴分别交于点A和点B,且OA=OB=1.这条曲线是函数