题目内容
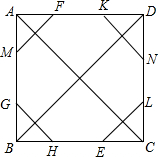 如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.
如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.考点:作图—应用与设计作图
专题:
分析:利用正方形的性质进而得出AF=AM,再利用等腰直角三角形的性质求出八边形的内角以及边长即可得出答案.
解答: 解:如图:设AO=a,则AB=BC=CD=AD=
解:如图:设AO=a,则AB=BC=CD=AD=
a,
∵AK=AG=AO=CH=CN=DF=BM=BE=DL,AB=BC=CD=AD,
∴AF=AM=
a-a,∠AFM=∠AMF=45°,
则MF=2a-
a,∠MFK=∠FMG=135°,
故可得,∠MFK=∠FMG=∠FKN=∠KNL=∠NLE=∠LEH=∠EHG=∠HGM=135°,
故FK=AD-AF-KD=
a-(
a-a)-(
a-a)=2a-
a,
故可得:MG=MF=FK=KN=NL=EL=HE=GH,
故木工的作图可得到一个八边形.
 解:如图:设AO=a,则AB=BC=CD=AD=
解:如图:设AO=a,则AB=BC=CD=AD=| 2 |
∵AK=AG=AO=CH=CN=DF=BM=BE=DL,AB=BC=CD=AD,
∴AF=AM=
| 2 |
则MF=2a-
| 2 |
故可得,∠MFK=∠FMG=∠FKN=∠KNL=∠NLE=∠LEH=∠EHG=∠HGM=135°,
故FK=AD-AF-KD=
| 2 |
| 2 |
| 2 |
| 2 |
故可得:MG=MF=FK=KN=NL=EL=HE=GH,
故木工的作图可得到一个八边形.
点评:此题主要考查了应用设计与作图,熟练应用正方形的性质得出各边与角的度数是解题关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
在△ABC中,已知∠A、∠B、∠C的度数之比是6:5:1,则△ABC的形状是( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
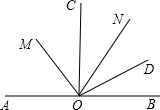 如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.
如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.