题目内容
已知正三角形的边长为6,剪去三个角后得到一个正六边形,求六边形的边长和面积.
考点:正多边形和圆
专题:
分析:本题需先根据已知条件得出大三角形的各边长相等,再根据截去的三角形也是等边三角形,即可求出正六边形的边长;连接OA,OB,过点O作OD⊥AB于点D,根据正六边形的性质可知△OAB是等边三角形,故可得出其面积,进而得出结论.
解答: 解:∵正三角形的边长为6cm,
解:∵正三角形的边长为6cm,
∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2.
连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB=
=60°,
∴△OAB是等边三角形,
∴OD=OA•sin60°=2×
=
,
∴S△OAB=
×2×
=
,
∴S六边形=6S△OAB=6
.
 解:∵正三角形的边长为6cm,
解:∵正三角形的边长为6cm,∴3个边长都相等,
又∵截去三个小等边三角形,
∴各个小三角形的边长也相等,
∴正六边形的边长为:2.
连接OA,OB,过点O作OD⊥AB于点D,
∵∠AOB=
| 360° |
| 6 |
∴△OAB是等边三角形,
∴OD=OA•sin60°=2×
| ||
| 2 |
| 3 |
∴S△OAB=
| 1 |
| 2 |
| 3 |
| 3 |
∴S六边形=6S△OAB=6
| 3 |
点评:本题主要考查的是正多边形和圆,熟知等边三角形的性质及正六边形的性质是解题的关键.

练习册系列答案
相关题目
下列判断正确的是( )
| A、四边形的外角和大于内角和 |
| B、一个多边形的内角和为1880° |
| C、一个多边形的内角中,锐角的个数可以任意多 |
| D、若多边形边数从3增加到n(n为大于3的自然数),它们的外角和度数不变 |
 图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )| A、甲先到B点 |
| B、乙先到B点 |
| C、甲、乙同时到B |
| D、无法确定 |
下列各式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知一次函数y=(2-m)x+3中,函数值y随自变量x的增大而减小,那么m的取值范围是( )
| A、m≤2 | B、m≥2 |
| C、m<2 | D、m>2 |
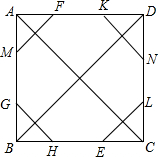 如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.
如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.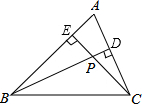 如图,在△ABC中,高BD和CE相交于点P.
如图,在△ABC中,高BD和CE相交于点P.