题目内容
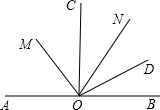 如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.
如图,∠AOC=90°,ON是锐角∠COD的平分线,OM是∠AOD的平分线,求∠MON的度数.考点:角的计算
专题:
分析:根据余角的性质,可得∠COD与∠BOD的关系,根据补角的性质,可得∠AOD与∠BOD的关系,根据角平分线的性质,可得∠MOD,∠DON,根据角的和差,可得答案.
解答:解:由余角的性质,得
∠COD=90°-∠BOD.
由邻补角的性质,得
∠AOD=180°-∠BOD.
由ON是锐角∠COD的平分线,OM是∠AOD的平分线,得
∠DON=
∠COD═
×(90°-∠BOD)=45°-
∠BOD,
∠MOD=
∠AOD=
×(180°-∠BOD)=90°-
∠BOD.
由角的和差,得
∠MON=∠MOD-∠DON
=(90°-
∠BOD)-(45°-
∠BOD)
=90°-
∠BOD-45°-
∠BOD
=45°.
∠COD=90°-∠BOD.
由邻补角的性质,得
∠AOD=180°-∠BOD.
由ON是锐角∠COD的平分线,OM是∠AOD的平分线,得
∠DON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠MOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由角的和差,得
∠MON=∠MOD-∠DON
=(90°-
| 1 |
| 2 |
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
| 1 |
| 2 |
=45°.
点评:本题考查了角的计算,利用了余角、补角的性质,角平分线的性质,角的和差.

练习册系列答案
相关题目
在入学体验的过程中,测得张亮同学的体重约为48kg,则张亮同学的实际体重x(kg)的取值范围为( )
| A、47.5 kg<x<48.5 kg |
| B、47 kg<x<49 kg |
| C、47.5 kg≤x<48.5 kg |
| D、47.5 kg<x≤48.5 kg |
下列判断正确的是( )
| A、四边形的外角和大于内角和 |
| B、一个多边形的内角和为1880° |
| C、一个多边形的内角中,锐角的个数可以任意多 |
| D、若多边形边数从3增加到n(n为大于3的自然数),它们的外角和度数不变 |
 图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )
图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB1路线爬行,则下列结论正确的是( )| A、甲先到B点 |
| B、乙先到B点 |
| C、甲、乙同时到B |
| D、无法确定 |
等腰三角形的周长是31,其中一边长为7cm,等腰三角形的底边长是( )
| A、12cm | B、7cm |
| C、17cm | D、7cm或17cm |
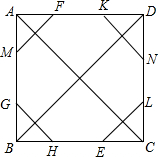 如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由.
如图,木工要用一个正方形木板制成一个正八边形采取了如下方式作图:先确定正方形ABCD的中心O,再分别以A、B、C、D为圆心,AO为半径作弧和各边相交于F、M、E、H、G、L、N、K,你认为木工的作图可得到一个八边形吗?若能,试证明;若不能,说明理由. 如图,PA切⊙O于点P,AB交⊙O于C,B两点,求证:∠APC=∠B.
如图,PA切⊙O于点P,AB交⊙O于C,B两点,求证:∠APC=∠B.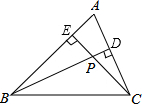 如图,在△ABC中,高BD和CE相交于点P.
如图,在△ABC中,高BD和CE相交于点P.