题目内容
6.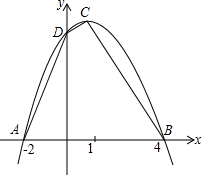 已知,如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9,求二次函数的解析式.
已知,如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9,求二次函数的解析式.
分析 根据函数图象过点(-2,0)和(4,0)可得对称轴为x=1,又函数的最大值为9,则顶点的纵坐标为9,所以可设y=a(x-1)2+9,再把点B的坐标代入求出a的值即可.
解答 解:由抛物线的对称性知,它的对称轴是x=1.
又∵函数的最大值为9,
∴抛物线的顶点为C(1,9).
设抛物线的解析式为y=a(x-1)2+9,代入B(4,0),求得a=-1.
∴二次函数的解析式是y=-(x-1)2+9,
即y=-x2+2x+8.
点评 本题考查了待定系数法求二次函数解析式:二次函数的解析式有三种常见形式:一般式:y=ax2+bx+c(a,b,c是常数,a≠0); 顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标; 交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0).

练习册系列答案
相关题目
16.在具备下列条件的四边形中,相似的是( )
| A. | 四边对应成比例的两个直角梯形 | B. | 四边对应成比例的两个等腰梯形 | ||
| C. | 四边对应成比例的两个菱形 | D. | 四边对应成比例的两个矩形 |
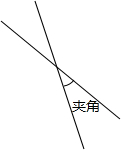 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问: