题目内容
18．a＜0，b＞0，则化简$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$；化简$\sqrt{（2-\sqrt{5}）^{2}}$=$\sqrt{5}$-2．分析 根据a＜0，b＞0，把二次根式$\sqrt{{a}^{2}b}$进行化简；根据2-$\sqrt{5}$＜0即可得出$\sqrt{{（2-\sqrt{5}）}^{2}}$的值．
解答 解：∵a＜0，b＞0，
∴$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$；
∵$\sqrt{5}$＞2，
∴2-$\sqrt{5}$＜0，
∴$\sqrt{{（2-\sqrt{5}）}^{2}}$=$\sqrt{5}$-2．
故答案为：-a$\sqrt{b}$，$\sqrt{5}$-2．
点评 本题考查的是二次根式的化简求值，熟知二次根式具有非负性是解答此题的关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
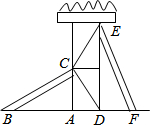如图，幼儿园的滑梯有两个长度相等滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等．
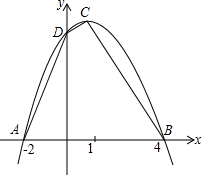已知，如图，二次函数的图象与x轴交于A（-2，0），B（4，0）两点，且函数的最大值为9，求二次函数的解析式．
13．方程$\frac{1}{x}$-2=x2-2x有（ ）个实数根．
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
下图是一个简单的数值运算程序，当输入x的值为-2时，则输出的数值为12．