题目内容
5. 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25m,与亭子距离CE=20m,小丽从楼房顶测得E点的俯角为45°.求:
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25m,与亭子距离CE=20m,小丽从楼房顶测得E点的俯角为45°.求:(1)点E到AB的距离;
(2)楼房AB的高.
分析 (1)过点E作EG⊥AB于G,过点E作EF⊥BC交BC的延长线于F,根据矩形的性质得到EF=BG,FB=EG,在Rt△ECF中,tan∠ECF=$\frac{\sqrt{3}}{3}$,求得∠ECF=30°,解直角三角形即可得到结论;
(2)根据小丽从楼房顶测得E点的俯角为45°,求得∠FAE=∠FEA=45°,于是得到AF=EF=20+10$\sqrt{3}$(m),根据得到结论.
解答 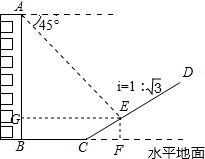 解:(1)过点E作EG⊥AB于G,
解:(1)过点E作EG⊥AB于G,
过点E作EF⊥BC交BC的延长线于F,
∵四边形EFBG是矩形,
∴EF=BG,FB=EG,
∵在Rt△ECF中,tan∠ECF=$\frac{\sqrt{3}}{3}$,
∴∠ECF=30°,
∵CE=20 m,
∴EF=10m,CF=10$\sqrt{3}$m,
∵BC=25m,
∴BF=BC+CF=25+10$\sqrt{3}$(m),
∴EG=25+10$\sqrt{3}$ (m)
∴点E到AB的距离是(25+10$\sqrt{3}$ )m;
(2)∵小丽从楼房顶测得E点的俯角为45°,
∴∠FAE=∠FEA=45°
∴AF=EF=20+10$\sqrt{3}$(m),
∵FB=EG=10 m,
∴AB=AF+FB=20+10$\sqrt{3}$+10=30+10$\sqrt{3}$(m)
∴楼房AB的高是(30+10$\sqrt{3}$)m.
点评 本题考查了解直角三角形的应用--仰角俯角问题、坡度坡角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
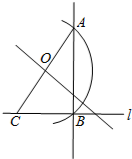 陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)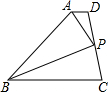 如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )