题目内容
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
① 当x取什么值时,y>0 ?
② 当x取什么值时,y的值随x的增大而减小?
(1)抛物线的解析式为y=-x2+2x+3;(2)抛物线与x轴的交点坐标(-1,0),(3,0);(3)详见解析;(4)①当-1<x<3时,y>0;②当x>1时,y的值随x的增大而减小.
【解析】
试题分析:(1)将(0,3)代入y=-x2+(m-1)x+m求得m,即可得出抛物线的解析式;
(2)令y=0,求得与x轴的交点坐标;令x=0,求得与y轴的交点坐标;
(3)得出对称轴,顶点坐标,画出图象即可;
(4)当y>0时,即图象在一、二象限内的部分;当y<0时,即图象在一、二象限内的部分;在对称轴的右侧,y的值随x的增大而减小.
试题解析:(1)∵抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点,
∴m=3,
∴抛物线的解析式为y=-x2+2x+3;
(2)令y=0,得x2-2x-3=0,
解得x=-1或3,
∴抛物线与x轴的交点坐标(-1,0),(3,0);
令x=0,得y=3,
∴抛物线与y轴的交点坐标(0,3);
(3)对称轴为x=1,顶点坐标(1,4),图象如图,

(4)如图,①当-1<x<3时,y>0;
当x<-1或x>3时,y<0;
②当x>1时,y的值随x的增大而减小.
考点:1.抛物线与x轴的交点;2.二次函数的图象;3.待定系数法求二次函数解析式.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目

 = .
= .


 AE,
AE,
 ,
, ,
,
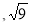 , -0.2,1.6,
, -0.2,1.6, , 0, 1.1010010001……(每两个1之间多一个0)
, 0, 1.1010010001……(每两个1之间多一个0)