��Ŀ����
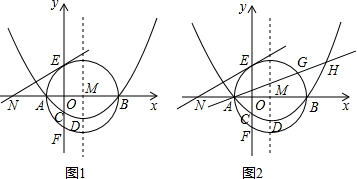
��֪����ͼ1��������y=ax2+bx+c��a��0��������A ��x1��0����B ��x2��0����C ��0��-2�����䶥��ΪD����ABΪֱ���ġ�M��y���ڵ�E��F����E�ڵ�F���Ϸ���������E����M�����߽�x���ڵ�N ��-6��0����
|x1-x2|=8��
��1���������ߵĽ���ʽ������D�����ꣻ
��2���ڣ�1���е����������Ƿ����һ��P�������D�غϣ���ʹ�á�ABP���ADB���ƣ������ڣ����P������ꣻ�������ڣ�˵�����ɣ�
��3����ͼ2����GΪ��M�ڵ�һ�����ڵ�����һ�㡢����AG��ֱ��l�루1���е������߽��ڵ�H�����H������Ϊ��m��n������AG•AH����m�ĺ�����ϵʽ������m=8ʱ���߶�GH�ij���
|x1-x2|=8��
��1���������ߵĽ���ʽ������D�����ꣻ
��2���ڣ�1���е����������Ƿ����һ��P�������D�غϣ���ʹ�á�ABP���ADB���ƣ������ڣ����P������ꣻ�������ڣ�˵�����ɣ�
��3����ͼ2����GΪ��M�ڵ�һ�����ڵ�����һ�㡢����AG��ֱ��l�루1���е������߽��ڵ�H�����H������Ϊ��m��n������AG•AH����m�ĺ�����ϵʽ������m=8ʱ���߶�GH�ij���

���㣺���κ����ۺ���
ר�⣺
��������1���������߽���ʽ����֪3�㣬�ֽ�֪C�㣬A��B�����䲻��ȷ������|x1-x2|=8���ɵ�AB=8����ΪEΪ�е㣬������Բ�����е��Ƕ�������Ŀ�ij������������������������ʣ���MO=x��EO=y�ù���x��y�ķ����飬��ü���A��B���꣬�����������������ã�
��2������ȷ����ABP���ADB������֪��Ӧ�㣬��ô��BAP=��DAB���ɴ˻�ͼ����һ��P������ʱ�ġ�ABP���ADB���ƣ���ôAB��BP�Ĺ�ϵ��ͬAD��DB��ϵһ�£���ΪAD=BD�����Խ����ж�BP�Ƿ����AB��֪��
��3��������е�AG•AH�������뵽�и��߶�������GH•AH=����H�����߳���ƽ������AH•AG=AH•��AH-GH��=AH2-GH•AH������A��̶���H����֪��AH2��������һ�㶼�����е���Բ�ĵ����ߣ�������ǡ�ù���ֱ�������Σ����ù��ɶ�����ת��������H�����߳���ƽ�����������ɱ�ʾ������ϵ����ù�ϵ��m=8�����뼴�ɣ������Ƶ�GH��
��2������ȷ����ABP���ADB������֪��Ӧ�㣬��ô��BAP=��DAB���ɴ˻�ͼ����һ��P������ʱ�ġ�ABP���ADB���ƣ���ôAB��BP�Ĺ�ϵ��ͬAD��DB��ϵһ�£���ΪAD=BD�����Խ����ж�BP�Ƿ����AB��֪��
��3��������е�AG•AH�������뵽�и��߶�������GH•AH=����H�����߳���ƽ������AH•AG=AH•��AH-GH��=AH2-GH•AH������A��̶���H����֪��AH2��������һ�㶼�����е���Բ�ĵ����ߣ�������ǡ�ù���ֱ�������Σ����ù��ɶ�����ת��������H�����߳���ƽ�����������ɱ�ʾ������ϵ����ù�ϵ��m=8�����뼴�ɣ������Ƶ�GH��
����⣺
��1��

��ͼ1������ME����OM=x��EO=y��
��N ��-6��0����|x1-x2|=8��
��NO=6��AB=8��
��EM=AM=MB=4��
�ߡ�ENO=90��-��NEO=��MEO����NOE=��EOM=90�㣬
���NEO�ס�EM0��
��
=
��
��
=
����y2=6x��
��Rt��EOM��
��EO2+OM2=EM2��
��y2+x2=42=16��
��x2+6x-16=0��
��x=2����x=-8����ֵ��ȥ����
��OM=2��
��A��-2��0����B��6��0����
����A��B��C�������꣬���������Ϊy=
x2-
x-2��
�ඥ��D��2��-
����
��2��

��ͼ2������AD��BD������PAB=��DAB��MD��Q������������P��
��ȻQ��D����x��Գƣ���Q��2��
����
���A��-2��0����Q��2��
����ֱ��Ϊy=kx+b��
�������꣬���ֱ��AQ��y=
x+
��
��P��x��y����������
��
���
����A�غ���ȥ������
��
��P��10��8����
��B��6��0����
��PB2=��xP-xB��2+��yP-yB��2=16+64=80��
��PB=4
��
��AB=8��
��AB��PB��
��AD=BD��
�����P��ʹ�á�ABP���ADB���ƣ�
��3��

��ͼ3������H����M������HI���е�ΪI������MI��HM��
���и��߶�����GH•AH=HI2��
��M��2��0����H��m��
m2-
m-2����
��MH2=��xH-xM��2+��yH-yM��2=��m-2��2+��
m2-
m-2��2��
��Rt��MHI��
��MI=4��
��HI2=MH2-MI2=��m-2��2+��
m2-
m-2��2-16��
��GH•AH=��m-2��2+��
m2-
m-2��2-16��
��A��-2��0����
��AH2=��xH-xA��2+��yH-yA��2=��m+2��2+��
m2-
m-2��2��
��AH•AG=AH•��AH-GH��=AH2-GH•AH=��m+2��2+��
m2-
m-2��2-[��m-2��2+��
m2-
m-2��2-16]=8m+16��
��m=8ʱ��AG•AH=8•8+16=80��
��m=8��
��H��8��
����
��AH2=��xH-xA��2+��yH-yA��2=��8+2��2+��
-0��2=
��
��AH=
��
��AG=
��
��GH=AH-AG=
��
��1��

��ͼ1������ME����OM=x��EO=y��
��N ��-6��0����|x1-x2|=8��
��NO=6��AB=8��
��EM=AM=MB=4��
�ߡ�ENO=90��-��NEO=��MEO����NOE=��EOM=90�㣬
���NEO�ס�EM0��
��
| NO |
| OE |
| EO |
| OM |
��
| 6 |
| y |
| y |
| x |
��Rt��EOM��
��EO2+OM2=EM2��
��y2+x2=42=16��
��x2+6x-16=0��
��x=2����x=-8����ֵ��ȥ����
��OM=2��
��A��-2��0����B��6��0����
����A��B��C�������꣬���������Ϊy=
| 1 |
| 6 |
| 2 |
| 3 |
�ඥ��D��2��-
| 8 |
| 3 |
��2��

��ͼ2������AD��BD������PAB=��DAB��MD��Q������������P��
��ȻQ��D����x��Գƣ���Q��2��
| 8 |
| 3 |
���A��-2��0����Q��2��
| 8 |
| 3 |
�������꣬���ֱ��AQ��y=
| 2 |
| 3 |
| 4 |
| 3 |
��P��x��y����������
|
���
|
|
��P��10��8����
��B��6��0����
��PB2=��xP-xB��2+��yP-yB��2=16+64=80��
��PB=4
| 5 |
��AB=8��
��AB��PB��
��AD=BD��
�����P��ʹ�á�ABP���ADB���ƣ�
��3��

��ͼ3������H����M������HI���е�ΪI������MI��HM��
���и��߶�����GH•AH=HI2��
��M��2��0����H��m��
| 1 |
| 6 |
| 2 |
| 3 |
��MH2=��xH-xM��2+��yH-yM��2=��m-2��2+��
| 1 |
| 6 |
| 2 |
| 3 |
��Rt��MHI��
��MI=4��
��HI2=MH2-MI2=��m-2��2+��
| 1 |
| 6 |
| 2 |
| 3 |
��GH•AH=��m-2��2+��
| 1 |
| 6 |
| 2 |
| 3 |
��A��-2��0����
��AH2=��xH-xA��2+��yH-yA��2=��m+2��2+��
| 1 |
| 6 |
| 2 |
| 3 |
��AH•AG=AH•��AH-GH��=AH2-GH•AH=��m+2��2+��
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
��m=8ʱ��AG•AH=8•8+16=80��
��m=8��
��H��8��
| 10 |
| 3 |
��AH2=��xH-xA��2+��yH-yA��2=��8+2��2+��
| 10 |
| 3 |
| 1000 |
| 9 |
��AH=
10
| ||
| 3 |
��AG=
12
| ||
| 5 |
��GH=AH-AG=
14
| ||
| 15 |
�����������ۺ��ѶȽϸߣ�������Ҳ�ϴ���Ҫ���������������ơ����������ʡ����ù��ɶ���������ϵ��������뼰Բ���и��߶�����֪ʶ�����������ʵķ�ʽ���ڶ����ڳ��濼����ֵ��ѧ����ϰ�����̣�������˵����һ�������ܸߵ���Ŀ��

��ϰ��ϵ�д�
�����Ŀ
�������5�����+5���ʾ����ô����3��ɱ�ʾΪ��������
| A��+3�� | B��-3�� |
| C��+3 | D��-3 |
��֪����ABC�У�AB=4��AC=3��BC=
�����ABC������ǣ�������
| 7 |
| A��6 | ||
| B��5 | ||
C��1.5
| ||
D��2
|
 ij�����꼶��3000��ѧ���μӡ���������֪ʶ���������
ij�����꼶��3000��ѧ���μӡ���������֪ʶ���������
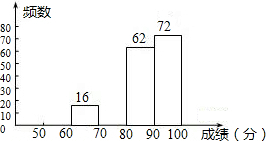
 2013��12��23�գ�����칫��ӡ�������������ͼ������������ļ�ֵ�۵�����������������24�ֺ��ļ�ֵ�۷ֳ�3�����棺��ǿ����������������г���ǹ��Ҳ���ļ�ֵĿ�ꣻ���ɡ�ƽ�ȡ����������Σ���������ļ�ֵȡ��������ҵ�����š����ƣ��ǹ�����˲���ļ�ֵ��ijУ���꼶��һ�������ѧ��ȤС��͡����˽����������ļ�ֵ���𣿡���������˱�У����ͬѧ�����Ե������������������Ƴ���ͼ�в�������ͳ��ͼ����
2013��12��23�գ�����칫��ӡ�������������ͼ������������ļ�ֵ�۵�����������������24�ֺ��ļ�ֵ�۷ֳ�3�����棺��ǿ����������������г���ǹ��Ҳ���ļ�ֵĿ�ꣻ���ɡ�ƽ�ȡ����������Σ���������ļ�ֵȡ��������ҵ�����š����ƣ��ǹ�����˲���ļ�ֵ��ijУ���꼶��һ�������ѧ��ȤС��͡����˽����������ļ�ֵ���𣿡���������˱�У����ͬѧ�����Ե������������������Ƴ���ͼ�в�������ͳ��ͼ����