题目内容
在Rt△ABC中，∠C=90°，∠A=50°，则∠B= ．
考点：三角形内角和定理
专题：
分析：根据直角三角形的两个锐角互余的性质进行解答．
解答：
解：∵Rt△ABC中，∠C=90°，∠A=50°，
∴∠A+∠B=90°（直角三角形的两个锐角互余），
∴∠B=40°．
故答案为：40°．
解：∵Rt△ABC中，∠C=90°，∠A=50°，∴∠A+∠B=90°（直角三角形的两个锐角互余），
∴∠B=40°．
故答案为：40°．
点评：本题考查了直角三角形的性质．解答该题时利用了直角三角形的性质：直角三角形的两个锐角互余．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图，AB是⊙O的弦，OC⊥OA，交AB与点P，且PC=BC，求证：BC是⊙O的切线．
如图，四边形ABCD中，E、G分别是一组对边AD、BC的中点，F、H分别是对角线BD、AC的中点，要使四边形EFGH为矩形，应添加的条件是（ ）| A、AB=CD |
| B、AB⊥CD |
| C、AC=BD |
| D、AC⊥BD |
如图，在凸四边形ABCD中，E、F分别是AD、BC边的中点，则AB+CD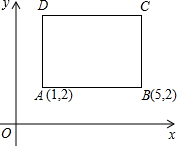
如图，四边形ABCD是一正方形，已知A（1，2），B（5，2）．
已知，四边形ABCD内接于⊙O，连结AC和BD交于点E，且AC平分∠BAD，求证：△ABC∽△BCE．
如图所示，请用不等号“＜”或“＞”表示∠1、∠2、∠3的大小关系：