Question

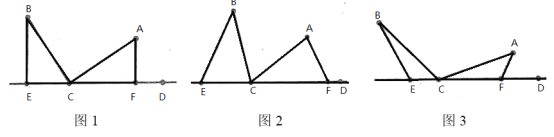
【题目】直线CD是经过∠BCA顶点C的一条直线，CA=CB，点E、F分别是直线CD上的两点，且∠BEC=∠CFA=∠BCA,

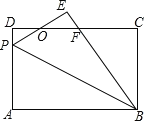
（1）如图1，当∠BCA=90时，则BE与CF的数量关系是：______________

（2）如图2，当∠BCA为锐角时，（1）中的数量关系是否依然成立？若成立，请证明

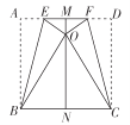
（3）如图 3，当∠BCA为钝角时，请说出EF、BE、AF三条线段的数量关系（不必证明）

Answer 1

【答案】（1）BE=CF; （2）成立，理由见解析；（3）EF=BE+AF

【解析】

（1）根据,可以得到,而由已知条件可以得到：，所以，那么，由此可以得到，结合已知条件，可以证明,所以；

（2）根据三角形的外角定理可以得到：,而，由此可以得到，再结合已知条件，可以证明，所以依然成立；

（3）按照和（2）同样的方法证明，那么，,所以;

（1）

又

又

（2）成立 ，理由是：

，

且

又

（3），理由如下：

，

且

又

，