Question

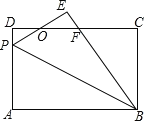
【题目】如图，已知长方形ABCD中，AD=6，AB=8，P是AD边上的点，将△ABP沿BP折叠，使点A落在点E上，PE、BE与CD分别交于点O、F，且OD=OE，则AP的长为(　　)

A.4.8B.5C.5.2D.5.4

Answer 1

【答案】A

【解析】

根据题意证明△ODP≌△OEF,再设出未知数,利用勾股定理列出方程解出即可．

∵四边形ABCD是长方形,

∴∠A=∠C=∠D=90°,CD=AB=8,BC=AD=6,

由折叠的性质得：EP=AP,BE=AB=8,∠E=∠A=90°,

在△ODP和△OEF中,,

∴△ODP≌△OEF(ASA),

∴PD=FE,OP=OF,

∴DF=EP=AP,

设AP=x,则DF=x,FE=PD=6﹣x,

∴CF=CD﹣DF=8﹣x,BF=BE﹣FE=x+2,

在Rt△BCF中,BC2+CF2=BF2,

即62+(8﹣x)2=(x+2)2,

解得：x=4.8．

故选：A．