题目内容
1.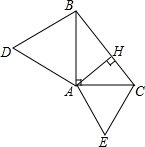 △ABC中,∠BAC=90°,分别以AB、AC为边,得到等边△ABD、等边△ACE.过A作AH⊥BC于点H.求证:
△ABC中,∠BAC=90°,分别以AB、AC为边,得到等边△ABD、等边△ACE.过A作AH⊥BC于点H.求证:(1)S△ABD:S△ACE=BH:CH;
(2)AE:AH=BD:BH;
(3)△ADH∽△CEH;
(4)判断DH和EH的关系.
分析 (1)根据等边三角形的性质得到AB=BD=AD,AC=CE=AE,∠3=∠4=∠5=∠8=60°,根据直角三角形的性质得到∠2=∠6,∠1=∠7,推出△ABH∽△ABC∽△ACH,于是得到$\frac{AB}{BC}$=$\frac{BH}{AB}$,$\frac{AC}{BC}=\frac{CH}{AC}$由等边△ABD∽等边△ACE,根据相似三角形的性质即可得到结论;
(2)根据相似三角形的性质得到$\frac{AC}{AH}=\frac{AB}{BH}$,由于AB=BD,AC=AE,等量代换即可得到结论;
(3)连接DH,EH,同(2)可证AC:HC=AB:AH,等量代换得到CE:HC=AD:AH,根据∠3=∠8,∠1=∠7,证得∠DAH=∠ECH,于是得到△ADH∽△CEH,根据相似三角形的性质得到∠AHD=∠CHE;
(4)同(3)可证:∠DBH=∠EAH,由于$\frac{AE}{AH}=\frac{BD}{BH}$,于是得到△BHD∽AHE,根据相似三角形的性质得到∠DHE=∠AHD+∠AHE=∠AHD+∠BHD=∠AHB=90°,即可得到结论.
解答 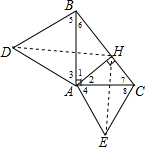 证明:(1)∵等边△ABD和△ACE,
证明:(1)∵等边△ABD和△ACE,
∴AB=BD=AD,AC=CE=AE,∠3=∠4=∠5=∠8=60°,
∵Rt△ABC,∠BAC=90°,AH⊥BC,
∴∠1+∠2=∠1+∠6=∠2+∠7=90°,
∴∠2=∠6,∠1=∠7,
∴△ABH∽△ABC∽△ACH,
∴$\frac{AB}{BC}$=$\frac{BH}{AB}$,$\frac{AC}{BC}=\frac{CH}{AC}$,
∴AB2=BC•BH,AC2=CH•BC,
∵等边△ABD∽等边△ACE,
∴$\frac{{S}_{△ABD}}{{S}_{△ACE}}$=$\frac{A{B}^{2}}{A{C}^{2}}$=$\frac{BC•BH}{BC•CH}$=$\frac{BH}{CH}$;
(2)∵△ABH∽△ACH,
∴$\frac{AC}{AH}=\frac{AB}{BH}$,
∵AB=BD,AC=AE,
∴AE:AH=BD:BH;
(3)连接DH,EH,同(2)可证AC:HC=AB:AH,
∴CE:HC=AD:AH,
∵∠3=∠8,∠1=∠7,
∴∠DAH=∠ECH,
∴△ADH∽△CEH,
∴∠AHD=∠CHE;
(4)同(3)可证:∠DBH=∠EAH,
∵$\frac{AE}{AH}=\frac{BD}{BH}$,
∴△BHD∽△AHE,
∴∠DHE=∠AHD+∠AHE=∠AHD+∠BHD=∠AHB=90°,
∴DH⊥EH.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,直角三角形的性质,正确的作出辅助线构造相似三角形是解题的关键.

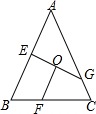 如图,在△ABC中,AB=AC,点E、F、G分别在边AB、BC、AC上,CG=BF,BE=CF,O是EG的中点,求证:FO⊥GE.
如图,在△ABC中,AB=AC,点E、F、G分别在边AB、BC、AC上,CG=BF,BE=CF,O是EG的中点,求证:FO⊥GE.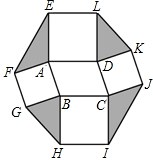 如图,以?ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果?ABCD的面积为8,则图中阴影部分四个三角形的面积和为( )
如图,以?ABCD的四条边为边,分别向外作正方形,连结EF,GH,IJ,KL.如果?ABCD的面积为8,则图中阴影部分四个三角形的面积和为( ) 如图,D是等边△ABC内一点,AD=2,BD=1,若将△ABD绕点A旋转后到△ACP位置,则DP的长是2.
如图,D是等边△ABC内一点,AD=2,BD=1,若将△ABD绕点A旋转后到△ACP位置,则DP的长是2.