题目内容
13.在平面直角坐标系中,设二次函数y1=(x+a)(x-a-1),其中a≠0.(1)若函数y1的图象经过点(1,-2),求函数y1的表达式;
(2)若一次函数y2=ax+b的图象与y1的图象经过x轴上同一点,探究实数a,b满足的关系式;
(3)已知点P(x0,m)和Q(1,n)在函数y1的图象上,若m<n,求x0的取值范围.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据函数图象上的点满足函数解析式,可得答案;
(3)根据二次函数的性质,可得答案.
解答 解:(1)函数y1的图象经过点(1,-2),得
(a+1)(-a)=-2,
解得a1=-2,a2=1,
函数y1的表达式y=(x-2)(x+2-1),化简,得y=x2-x-2;
函数y1的表达式y=(x+1)(x-2)化简,得y=x2-x-2,
综上所述:函数y1的表达式y=x2-x-2;
(2)当y=0时(x+a)(x-a-1)=0,解得x1=-a,x2=a+1,
y1的图象与x轴的交点是(-a,0),(a+1,0),
当y2=ax+b经过(-a,0)时,-a2+b=0,即b=a2;
当y2=ax+b经过(a+1,0)时,a2+a+b=0,即b=-a2-a;
(3)当P在对称轴的左侧(含顶点)时,y随x的增大而减小,
(1,n)与(0,n)关于对称轴对称,
由m<n,得0<x0≤$\frac{1}{2}$;
当时P在对称轴的右侧时,y随x的增大而增大,
由m<n,得$\frac{1}{2}$<x0<1,
综上所述:m<n,求x0的取值范围0<x0<1.
点评 本题考查了二次函数图象上点的坐标特征,解(1)的关键是利用待定系数法;解(2)的关键是把点的坐标代入函数解析式;解(3)的关键是利用二次函数的性质,要分类讨论,以防遗漏.

练习册系列答案
相关题目
4.下列算式的运算结果为a4的是( )
| A. | a4•a | B. | (a2)2 | C. | a3+a3 | D. | a4÷a |
8.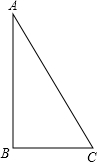 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )
 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )
如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的底面圆的周长分别记作l1,l2,侧面积分别记作S1,S2,则( )| A. | l1:l2=1:2,S1:S2=1:2 | B. | l1:l2=1:4,S1:S2=1:2 | ||
| C. | l1:l2=1:2,S1:S2=1:4 | D. | l1:l2=1:4,S1:S2=1:4 |
9.已知α是锐角,且点A($\frac{1}{2}$,a),B(sin30°+cos30°,b),C(-m2+2m-2,c)都在二次函数y=-x2+x+3的图象上,那么a、b、c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | c<b<a |
 解不等式组:$\left\{{\begin{array}{l}{-2x<6}\\{3({x-2})≤x-4}\end{array}}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{{\begin{array}{l}{-2x<6}\\{3({x-2})≤x-4}\end{array}}\right.$,并把解集在数轴上表示出来.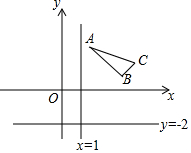 如图,△ABC的顶点分别为A(2,3),B(4,1),C(5,2),分别作出△ABC关于直线x=1对称的图形△A1B1C1和关于直线y=-2对称的图形△A2B2C2.
如图,△ABC的顶点分别为A(2,3),B(4,1),C(5,2),分别作出△ABC关于直线x=1对称的图形△A1B1C1和关于直线y=-2对称的图形△A2B2C2.