如图.在一张矩形硬纸板中剪下一个半圆形和一个圆形.使之恰好围成一个圆锥.则这个圆锥的侧面积S侧和底面积S底的关系是( )A．S侧=S底B．S侧=2S底C．S侧=3S底D．S侧=4S底题目和参考答案——青夏教育精英家教网—

题目内容

4．

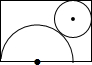如图，在一张矩形硬纸板中剪下一个半圆形和一个圆形，使之恰好围成一个圆锥，则这个圆锥的侧面积S_侧和底面积S_底的关系是（　　）

A．

S_侧=S_底

B．

S_侧=2S_底

C．

S_侧=3S_底

D．

S_侧=4S_底

分析设半圆的半径为R，小圆的半径为r，根据侧面展开图扇形的弧长=底面圆周长，列出方程解得R=2r，由此即可解决问题．

解答解：设半圆的半径为R，小圆的半径为r，
由题意：$\frac{1}{2}$•2πR=2πr
∴R=2r，
∴S_侧：S_底=$\frac{1}{2}$•π•（2r）²：πr²=2：1．
故选B．

点评本题考查圆锥的有关知识、利用侧面展开图扇形的弧长=底面圆周长是解决问题的关键，属于基础题，中考常考题型．

练习册系列答案

相关题目

14．如果直线a、直线b都和直线c平行，那么直线a和直线b的位置关系是（　　）

15．

如图，一张宽度相等的纸条，折叠后，若∠ABC=120°，则∠1的度数为60°．

12．阅读下列材料并解决有关问题：
我们知道|x|=$\left\{{\begin{array}{l}{x（x＞0）}\\{0（x=0）}\\{-x（x＜0）}\end{array}}\right.$，现在我们可以用这一结论来化简含有绝对值的代数式，如化简代数式|x+1|+|x-2|时，可令x+1=0和x-2=0，分别求得x=-1，x=2（称-1，2分别为|x+1|与|x-2|的零点值）．在有理数范围内，零点值x=-1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况：（1）x＜-1；（2）-1≤x＜2；（3）x≥2．
从而化简代数式|x+1|+|x-2|可分以下3种情况：
（1）当x＜-1时，原式=-（x+1）-（x-2）=-2x+1；
（2）当-1≤x＜2时，原式=x+1-（x-2）=3；
（3）当x≥2时，原式=x+1+x-2=2x-1．
通过以上阅读，请你解决以下问题：
（1）分别求出|x+2|和|x-4|的零点值；
（2）化简代数式|x+2|-|x-4|；
（3）解方程|x-1|+|x+3|=6．

19．

如图所示，△ABC中，AC=AD=BD，∠DAC=80°，则∠B的度数是（　　）

9．

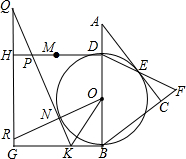如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长，交BC的延长线于点F，CF=1，cos∠ABC=$\frac{3}{5}$．
（1）求证：DE=EF；
（2）求⊙O的半径；
（3）以BD为边作正方形BDHC，M是HD的中点，P是线段MH上的一个动点（不与点M，H重合），过点P作⊙O的切线，交BG于点K切点为N．
①设DP=x，BK=y，求xy的值；
②GH的延长线与KP的延长线相交于点Q，连接ON并延长，交HG于点R，连接OK，请问是否存在点P，使△BKO∽△NRQ？若存在，试求①中x和y的值；若不存在，请说明理由．

16．方程$\sqrt{2x+1}+1=k$无实数根，则k的取值范围为k＜1．

13．

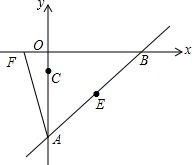如图，已知点A（0，a），B（b，0），C（0，c），且|a+4|+$\sqrt{{b^2}-8b+16}$=0，（c+1）²≤0，点D与点C关于直线AB对称，
（1）求直线AB的解析式和点C、D的坐标；
（2）点E在直线AB上，直接写出|EO-ED|的最大值和最小值及对应的点E的坐标；
（3）点F（-1，0），在平面内有一点P，使得△OAP∽△DAF，求点P的坐标．

14．

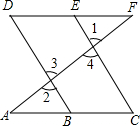如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证：
①BD∥CE
②DF∥AC．

试题分类