题目内容
2.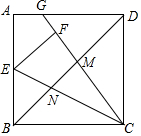 如图,正方形ABCD中,E为边AB上的中点,连接CE,将△BEC翻折,使点B落在点F处,对角线BD与CF,CE分别交于点N,M,CF的延长线与AD交于点G,如果正方形边长为4,则线段MN的长为$\frac{20\sqrt{3}}{7}$.
如图,正方形ABCD中,E为边AB上的中点,连接CE,将△BEC翻折,使点B落在点F处,对角线BD与CF,CE分别交于点N,M,CF的延长线与AD交于点G,如果正方形边长为4,则线段MN的长为$\frac{20\sqrt{3}}{7}$.
分析 连接EG,由E为边AB上的中点,得到AE=BE=$\frac{1}{2}$AB=2,根据全等三角形的性质得到AG=GF,设AG=GF=x,根据勾股定理得到AG=GF=1,求得DG=3,根据相似三角形的性质即可得到结论.
解答 解:连接EG,
∵E为边AB上的中点,
∴AE=BE=$\frac{1}{2}$AB=2,
∵将△BEC翻折,使点B落在点F处,
∴EF=BE=2,∠A=∠EFC=∠EFG=90°,
在Rt△AEG与Rt△EFG中,$\left\{\begin{array}{l}{AE=EF}\\{EG=GE}\end{array}\right.$,
∴Rt△AEG≌Rt△EFG,
∴AG=GF,
设AG=GF=x,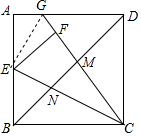
∴DG=4-x,CG=4+x,
∵DG2+CD2=CG2,
∴(4-x)2+42=(4+x)2,
∴x=1,
∴AG=GF=1,
∴DG=3,
∵BD=$\sqrt{2}$BC=4$\sqrt{2}$,
∵DG∥BC,
∴△DGM∽△BCM,
∴$\frac{DM}{BM}=\frac{DG}{BC}$=$\frac{3}{4}$,
∴DM=$\frac{12\sqrt{3}}{7}$,
同理BN=$\frac{4\sqrt{3}}{3}$,
∴MN=BD-BN-DM=$\frac{20\sqrt{3}}{7}$,
故答案为:$\frac{20\sqrt{3}}{7}$.
点评 本题考查了翻折变换-折叠问题,正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
10. 如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )
如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )
 如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )
如图所示,已知OC平分∠AOB,CD∥OB,若OD=4cm,则CD等于( )| A. | 1.5cm | B. | 2cm | C. | 3cm | D. | 4cm |
 在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,点D关于直线
在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,点D关于直线 A、B两城相距600千米,甲、乙两车从A城出发驶向B城,乙车的速度为75千米/时,甲车先走100千米乙车才出发,甲车到达B卸完货后立即返回A城,如图它们离A城的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.
A、B两城相距600千米,甲、乙两车从A城出发驶向B城,乙车的速度为75千米/时,甲车先走100千米乙车才出发,甲车到达B卸完货后立即返回A城,如图它们离A城的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.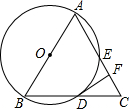 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作⊙O的切线,交AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作⊙O的切线,交AC于F.