题目内容
9.设a<b<c,实数m、n(m>n)满足2m+2n=a+b+c,2mn=ac,请将a、b、c、m、n按从小到大的顺序排列为n<a<b<m<c.分析 假设:a=2,b=4,c=6,计算m+n=6,mn=6,解方程组得出m和n的近似值,并根据各数值比较大小.
解答 解:假设:a=2,b=4,c=6,
则2m+2n=2+4+6=12;2mn=2×6=12,
∴m+n=6,mn=6,
解得:m=3+$\sqrt{3}$≈3+1.73=4.73,n=3-$\sqrt{3}$≈3-1.73=1.27,
∴n<a<b<m<c,
故n<a<b<m<c.
点评 本题考查了实数的大小比较,大小比较的方法有较多:①平方法,②倒数法,③特殊值法等,本题利用了特殊值法进行比较.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
19.若3m=2,3n=5,则3m+n的值是( )
| A. | 7 | B. | 90 | C. | 10 | D. | a2b |
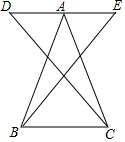 已知,如图,DE∥BC,点A是DE上一点,AD=AE,AB=AC.求证:∠D=∠E.
已知,如图,DE∥BC,点A是DE上一点,AD=AE,AB=AC.求证:∠D=∠E.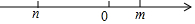 对于有理数m,n,定义一种新运算,规定m?n=|m+n|-|m-n|
对于有理数m,n,定义一种新运算,规定m?n=|m+n|-|m-n|