题目内容
13.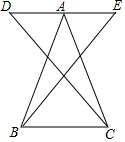 已知,如图,DE∥BC,点A是DE上一点,AD=AE,AB=AC.求证:∠D=∠E.
已知,如图,DE∥BC,点A是DE上一点,AD=AE,AB=AC.求证:∠D=∠E.
分析 由条件可证明△DAC≌△EBA,可证得∠ACD=∠ABE,则可求得∠EBC=∠DCB,再由平行的性质可求得∠D=∠E.
解答 证明:
∵AB=AC,
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠DAB=∠ABC,∠EAC=∠ACB,
∴∠DAB=∠EAC,
∴∠DAC=∠EAB,
在△ACD和△ABE中
$\left\{\begin{array}{l}{AC=AB}\\{∠DAC=∠EAB}\\{AD=AE}\end{array}\right.$
∴△ACD≌△ABE(SAS),
∴∠ABE=∠ACD,
∴∠EBC=∠DCB,
∵DE∥BC,
∴∠D=∠DCB,∠E=∠EBC,
∴∠D=∠E.
点评 本题主要考查等腰三角形的性质及全等三角形的判定和性质,由条件通过证明三角形全等证得∠ABE=∠ACD是解题的关键.

练习册系列答案
相关题目
1.下列计算中正确的有( )个
①3x2+x2=4x4②3x2-x2=3③5a2b-6ba2=-a2b④-7a2=-14a.
①3x2+x2=4x4②3x2-x2=3③5a2b-6ba2=-a2b④-7a2=-14a.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
18.下面图形中,为中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,该图形折叠成正方体后,与“沉”字相对的字是考.
如图,该图形折叠成正方体后,与“沉”字相对的字是考.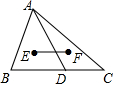 如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.
如图,在△ABC中,点D是BC上一点,E、F分别是△ABD、△ACD的重心,若BC=6,则线段EF的长为2.